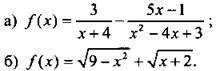
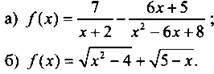
Не понятно чему равна первая функция, поэтому напишу просто как решить. Если графики функций пересекаются значит у них обоих имеется одна и таже общая точка, т.е.координаты этой точки удовлетворяют обоим уравнениям. Теперь чтобы найти эту точку делаем следующее: из любого уравнения выражаем какую-либо неизвестную через другую, н-р, я выражу из второго уравнения х. 3x+5y=-12
3х=-12-5у
х=(-12-5у)/3
Затем в другое уравнение вместо х подставляем полученное выражение
2( (-12-5у)/3 )-3y = (тут уж я не знаю чему там у тебя равно) Преобразуем выражение и находим у
(-24-10у)/3 - 3у= (дальше я преобразовать не могу так не знаю числа стоящего после равно)
Нашли у ( должно получиться какое-нибудь число)
Полученное число нужно подставить в выделенное выражение и получим х. Данные два числа записываем как координаты точки (х,у)
sin315°= sin(360°-45°)= -sin(45°) // тут стоит минус, так как наша функция находится в 4-ой четверти, синус это же игрек на системе координат, а игрек в 4-ой четверти отрицательный.
2 | 1
3 | 4
схематичная система координат )) тут я показал где находятся четверти.
cos315°= cos(360°-45°)= +cos45° // тут стоит плюс, так как косинус это икс и он в 4-ой четверти положительный.
tg(315°) = tg(360°-45°)= -tg(45°) // тут стоит минус, так как тангенс в 4-ой четверти отрицательный, тангенс это sin÷cos или y÷x, в нашем случаи будет так: tg(360°-45°)= -sin45°÷cos45°= -tg45°
ctg(315°) = ctg(360°-45°)= -ctg(45°) // тут все тоже самое, что и в tg , но только катангес это cos÷sin или x÷y => ctg(360°-45°)= cos45°÷(-sin45°)=
-ctg45°