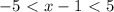
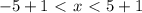
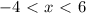
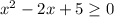
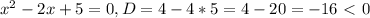
:
- парабола ветвями вверх, то неравенство выполняется для любых х.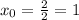
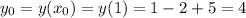
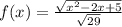принимает в вершине параболы х=1: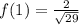
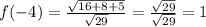
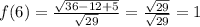
(0;4)
Объяснение:
А(-1;1), O(0;0), B(t;t²), t>0
Обозначение {AB}-вектор AB
{OA}={-1;1}; {OB}={t;t²}
OA=|{OA}|=√((-1)²+1²)=√2
OB=|{OB}|=√(t²+(t²)²)=t√(t²+1)
{OA}·{OB}=|{OA}|·|{OB}|·cosAOB
{-1;1}·{t;t²}=√2·t√(t²+1)·cosAOB
-t+t²=√2·t√(t²+1)·cosAOB
t-1=√(2(t²+1))·cosAOB
cosAOB=(t-1)/√(2(t²+1))
sinAOB=√(1-cos²AOB)=√(1-((t-1)/√(2(t²+1)))²)=√(1-(t-1)²/(2(t²+1)))=(t+1)/√(2(t²+1))
S(AOB)=0,5OA·OB·sinAOB=0,5·√2·t√(t²+1)·(t+1)/√(2(t²+1)))=0,5t(t+1)=10
t²+t=20
t²+t-20=0
(t-4)(t+5)=0
t>0⇒t=4
B(4; 16)
Уравнение прямой проходящей через точки M(a;b) и N(c;d) задается формулой
(x-a)/(c-a)=(y-b)/(d-b)
Уравнение прямой проходящей через точки А(-1;1) и B(4; 16) задается формулой
(x+1)/(4+1)=(y-1)/(16-1)
(x+1)/5=(y-1)/15
y-1=3(x+1)
y=3x+4
Координаты точки пересечения этой прямой с осью ординат C(o;y)
y=3·0+4=4
C(0;4)
хз что сюда написать, вот, да
Объяснение:
надеюсь всё ясно написала