35.
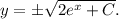
37.
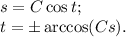
39.
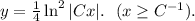
Объяснение:
35.
Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. В исходном случае переменные уже разделены, поэтому можно непосредственно проинтегрировать обе части уравнения:
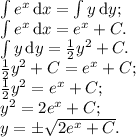
ответом будет являться найденная функция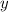 
.
37.
Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. Разделим переменные:
Теперь можно непосредственно проинтегрировать обе части уравнения:
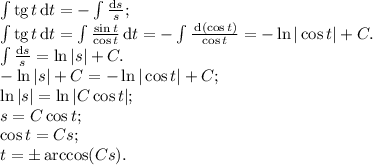
Не знаю, что здесь функция, а что переменная, так что в ответе будут в явном виде и s, как если бы переменной была t, и t, как если бы переменной была s.
39.
Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. Разделим переменные:
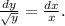
Теперь можно непосредственно проинтегрировать обе части уравнения:
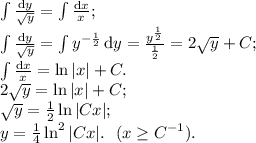
ответом будет являться найденная функция 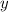с условием.
y=-0,4x²+2,4
0,4x²=2,4-y
0,4x²=y+2,4
x²=5/2y+6
Это ПАРАБОЛА