Чтобы понять решение линейных неравенств, рассмотрим пример: Как видно из решения, мы используем уже известные нам с 5ого класса навыки переноса x в левую часть. Это неравенство отличается от линейного уравнения только знаком >. Стоит также отметить, что ответ на решение записывается в неравенствах в виде промежутка. В нашем случае так: x∈(2; +∞). Круглая скобка показывает, что точка не включена в промежуток.
Рассмотрим другой пример: Как видно из решентя, мы меняем знак неравенства на противоположный при домножении обоих его частей на отрицательное число. ответ к неравенству запишем так: x∈[-1; +∞).
Чтобы закрепить материал попробуйте решить два неравенства, а потом сверить ответы: ответ: x∈[-2 4/9; +∞).
ответ: x∈(1 1003/4925; +∞).
Система неравенств решается так: Т. е. сначала решаем два неравенста как будто системы нет.
Теперь ищем общую часть. Она и будет являться ответом. У нас это: x∈(4, 7).
Чтобы понять решение линейных неравенств, рассмотрим пример: Как видно из решения, мы используем уже известные нам с 5ого класса навыки переноса x в левую часть. Это неравенство отличается от линейного уравнения только знаком >. Стоит также отметить, что ответ на решение записывается в неравенствах в виде промежутка. В нашем случае так: x∈(2; +∞). Круглая скобка показывает, что точка не включена в промежуток.
Рассмотрим другой пример: Как видно из решентя, мы меняем знак неравенства на противоположный при домножении обоих его частей на отрицательное число. ответ к неравенству запишем так: x∈[-1; +∞).
Чтобы закрепить материал попробуйте решить два неравенства, а потом сверить ответы: ответ: x∈[-2 4/9; +∞).
ответ: x∈(1 1003/4925; +∞).
Система неравенств решается так: Т. е. сначала решаем два неравенста как будто системы нет.
Теперь ищем общую часть. Она и будет являться ответом. У нас это: x∈(4, 7).
а
минусы сокращаются тогда:
б
3 ÷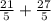 ÷
÷ 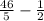 ÷
÷ 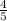 =
=  +
+ 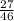 -
- 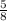 =
=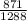
в
7x-63-3x-1=9
4x=76
x=19
капееец как же это доооолго я умер