Пусть m — произвольное значение
функции y. Тогда равенство y=m окажется верным при
тех значениях m, при которых уравнение y=f(x) относительно х
имеет корни. Найдем множество значений m, при которых эти уравнения имеют корни. Тем самым мы найдем область значений функций у.
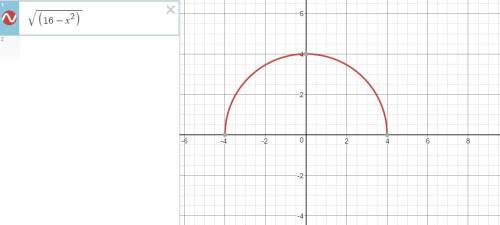
Возведем обе части уравнения √(16-x²)=m в квадрат и выразим x через m
1) m≥0;16-x²≥0⇒|x|≤4
16-x²=m²⇒x²-(16-m²)=0⇒|x|=√(16-m²)⇒√(16-m²)≤4⇒
|m|≤4;16-m²≤16⇒|m|≤4;m²≥0⇒m∈[0;4]
E(y)=[0;4] функция ограниченная
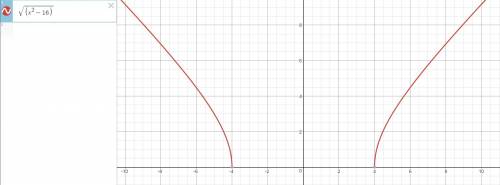
2) m≥0; x²-16≥0⇒|x|≥4
√(x²-16)=m⇒x²-16=m²⇒x²=m²+16⇒|x|=√(m²+16)⇒√(m²+16)≥4⇒
m²+16≥16⇒m²≥0⇒m≥0
E(y)=[0;∞) функция неограниченная
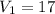км/ч - скорость велосипедиста
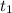ч - время, которое затратит велосипедист от момента выезда до момента встречи.
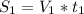км - расстояние ,которое проедет велосипедист от момента выезда до момента встречи, а это и есть расстояние от пункта А до места встречи.
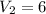км/ч - скорость пешехода
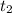ч - время, которое затратит пешеход от момента выхода до момента встречи. А т.к. пешеход вышел через 2 часа после выезда велосипедиста, то 
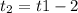ч 
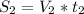км - расстояние ,которое пройдет пешеход от момента выхода до момента встречи. Т.е. это расстояние от пункта B до места встречи.
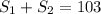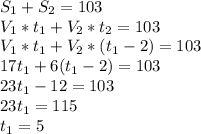
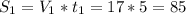км.
км
Два автомобиля проехали от пункта а до пункта б. Скорость второго автомобиля на 10км/ч меньше первого. Найдите скорость первого автомобиля, если первый автомобиль проехал за 5 часов, а второй за 6
Пусть х км/ч -скорость 1 автомобиля, тогда х-10 км/ч -скорость 2 автомобиля.
т.к. расстояние они проехали одинаковое, составляем уравнение:
5х=6(х-10)
5х=6х-60
5х-6х=-60
-х=-60
х=60
60км/ч - скорость первого автомобиля
ответ: 60 км/ч