Рассмотрим функцию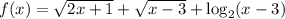 
на её области определения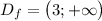 
График этой функции пересечёт линию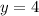 
более одного раза только если будут существовать промежутки разной монотонности (на каких-то функция возрастает, на других - убывает).
Обязательным условием смены монотонности функции является обращение её производной в ноль (или несуществование производной) в точке, где монотонность меняется. Попробуем их найти.
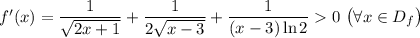
Как видно из вида производной, для всех точек области определения функции, она не обращается в ноль (более того, функция строго возрастает).
Таким образом, наше уравнение не может иметь более одного корня.
Методом пристального взгляда замечаем, что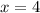 
- корень уравнения.
Действительно,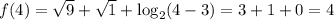 
ответ.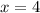
Уравнение имеет единственное решение: x = 4
Объяснение:
√(2х+1)+√(х-3)=4+log1/2 (x-3)
ОДЗ: x-3 > 0
Для удобства можно заменить: x-3 = t>0; 2x+1 = 2(t+3)+1 = 2t+7
√(2t+7)+√t - log1/2 t - 4 = 0
√(2t+7)+√t + log2 t - 4 = 0
Заметим, что при t > 0 функции: √(2t+7), √t, log2 t монотонно возрастают, а значит функция f(t) = √(2t+7)+√t + log2 t - 4 также монотонно возрастает. Таким образом, функция f(t) может принимать нулевое значение только в одной точке, иначе говоря, уравнение f(t) = 0 имеет не более одного решения.
Нетрудно заметить, что это решение существует: t = 1
Действительно, подставляя t = 1 в данное уравнение имеем:
√9+√1 + log2 1 - 4 = 0 - верно.
Возвращаемся к замене:
x-3 = 1
x = 4