Найдём ОДЗ логарифмов:
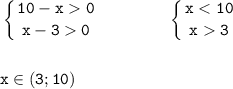
Для начала преобразуем каждое из выражений левой части, но сначала кое-что обсудим: мы можем обойтись и без этого вполне. Мы можем по свойству логарифмов преобразования суммы в произведение свести к логарифму по основанию 1/6. Но при раскрытии логарифмов с обеих сторон мы в любом случае сменим знак (так как при раскрытии логарифмов применяется неравенство, что если основание логарифма меньше единицы, то знак неравенства изменится на противоположный), как сделали это, приведя логарифмы к целому, не дробному основанию.
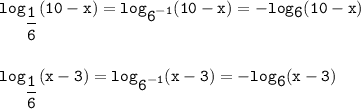
Затем сложим:
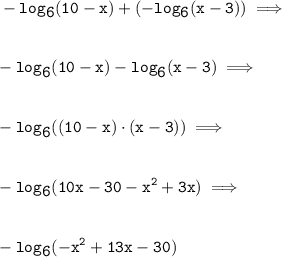
Умножим обе части на -1:
![\tt\displaystyle log_{\displaystyle6}(-x^{2}+13x-30)\leq 1\\\\\\log_{\displaystyle6}(-x^{2}+13x-30)\leq 6^{1}\\\\\\-x^{2}+13x-30 - 6 \leq 0\\\\\\x^{2}-13x+36\geq 0~~~~~~~~~~~~~~~~~~x^{2}-13x+36=0\\\\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~D=b^{2}-4\cdot a\cdot c = 169 -4\cdot 1\cdot 36=25=5^{2}\\\\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x_{1,2}=\frac{-b\pm\sqrt{D}}{2\cdot a}=\frac{13 \pm 5}{2}=9;~4\\\\\\(x - 9)\cdot(x - 4)\geq 0\\\\\\x\in(-\infty; 4]\cup[9; +\infty)](/tpl/images/0975/5264/73e32.png)
Объединим ОДЗ логарифмов и решение:
![\tt\displaystyle x\in(3; 10)~~~~~~~~~~and~~~~~~~~~~x\in(-\infty; 4]\cup[9; +\infty)\\\\\\x\in(3; 4]\cup[9;10)](/tpl/images/0975/5264/6e79f.png)
Пусть подмодульное выражение больше нуля:
x>0. Тогда функция приобретает вид
, при этом -1+3.5 x≠0, x≠2/7
Пусть теперь подмодульное выражение меньше нуля:
x<0. Тогда функция приобретает вид
, при этом -1-3.5 x≠0, x≠-2/7.
Построим график (см. приложенный файл) и отметим на нем выколотые точки: x≠-2/7 и x≠2/7
Очевидно, что прямая y=kx не будет иметь с графиком общих точек только в том случае, если будет проходить через выколотые точки. Определим угловой коэффициент k для случая x=-2/7 (соответствующее значение функции y = -3.5)
-3.5 = k*(-2/7), k = 49/4.
Определим угловой коэффициент k для случая x=2/7 (соответствующее значение функции y = -3.5)
-3.5 = k*(2/7), k = -49/4
ИЗВИНИТЕ НЕ МОГУ ПРИСЛАТЬ КАРТИНКУ.
3.4
Объяснение: