Вот накалякал. Разбирайся :)
xy/(x+y) = 5
xz/(x+z) = 7
yz/(y+z) = 9
xy = 5x + 5y
xz = 7x + 7z
yz = 9y + 9z
x(y-5) = 5y
x = 5y/(y-5)
5yz/(y-5) = 35y/(y-5) + 7z
5yz = 35y + 7z * (y-5)
5yz = 35y + 7yz - 35z
2yz + 35y = 35z
y(2z + 35) = 35z
y = 35z/(2z + 35) = z/(2z/35 + 1)
35z^2/(2z + 35) = 315z/(2z + 35) + 9z
35z^2 = 315z + 9z*(2z + 35)
35z^2 = 315z + 18z^2 + 315z
17z^2 = 630z
z=630/17
y = 35*630/(2*630/17 + 35)/17 = 35*630/(1260 + 595) = 22050/1855 = 630 / 53
x = 5*630/(630/53 - 5)/53 = 5*630/((630/53 - 5)*53) = 5*630/365 = 630/73
Объяснение:
6. данная функция является сложной. корень четной степени - это значит, что значение под корнем должно быть неотрицательным. т.е.
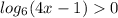решаем данное неравенство.
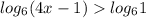
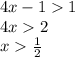
далее, функция логарифмическая, следовательно величина под знаком логарифма должна быть больше нуля.
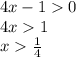
рассматриваем оба неравенства и находим область пересечения интервалов
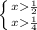x∈ [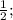 
+∞ [
7. 
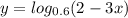значение под знаком логарифма должно быть больше нуля. 2-3х>0 2>3x x<2/3
рассмотрим условие при котором у>1
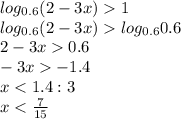
находим область пересечения обоих условий,
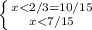x∈ ] -∞; 7/15 [
8. 
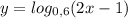область определения функции.
2х-1>0 x>1/2
вводим дополнительное условие
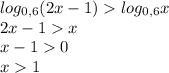
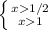x∈ ] 1; +∞ [
Объяснение:
а) это объединение множеств (-10;2)∪(-√5;+∞) включают в себя все элементы от -10 до +∞, т.е. (-10;+∞)
б) это пересечение множеств, в него входят только элементы, принадлежащие обоим множествам (-√5;6)∩(1;7)=(1;6)
в) (-∞;2.5)∪[2.5;+∞)=(-∞;+∞) здесь 2.5 не принадлежит первому интервалу, но принадлежит второму интервалу
г) (-3;√37)∩(-∞;6)=(-3;6)