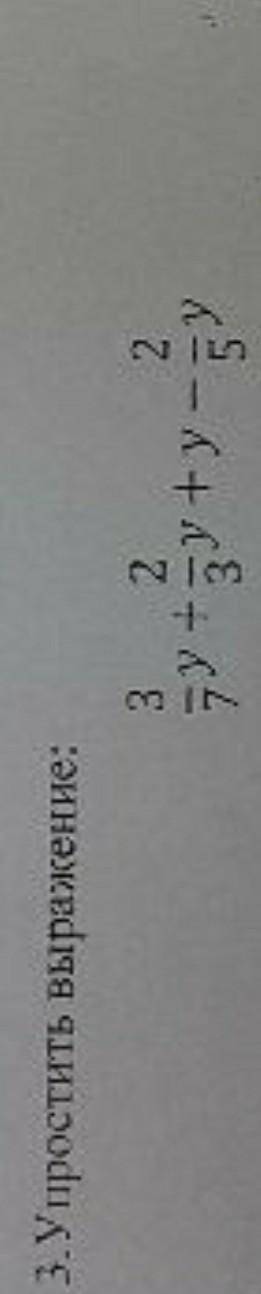
В решении.
Объяснение:
Задание 1.
Известно, что график функции f(x) проходит через точку (−5; 3) и параллелен графику функции y = −4x + 3.
а) Найдите уравнение данной функции f(x) ( ).
Графики линейных функций параллельны, если k₁ = k₂, а b₁ ≠ b₂.
k₁ = -4, значит, k₂ = -4;
Вычислить b₂:
Подставить в уравнение известные значения х и у (координаты точки) и вычислить b₂:
3 = -4 * (- 5) + b₂:
3 = 20 + b₂:
3 - 20 = b₂:
b₂ = -17;
Уравнение второй функции:
у = -4х - 17.
б) Постройте график данной функции f(x) ( ).
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
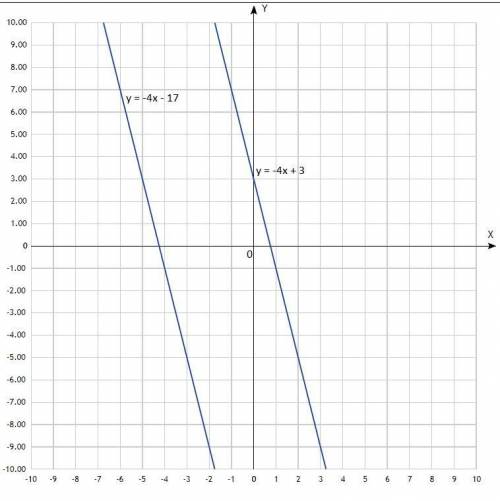
y = −4x + 3 у = -4х - 17
Таблицы:
х -1 0 1 х -6 -5 -4
у 7 3 -1 у 7 3 -1
По вычисленным точкам построить графики.
ответ:Рекуррентная формула — формула вида {\displaystyle a_{n}=f(n,a_{n-1},a_{n-2},\dots ,a_{n-p})}, выражающая каждый член последовательности a_n через p предыдущих членов и номер члена последовательности n.
Общая проблематика вычислений с использованием рекуррентных формул является предметом теории рекурсивных функций.
Рекуррентным уравнением называется уравнение, связывающее несколько подряд идущих членов некоторой числовой последовательности. Последовательность, удовлетворяющая такому уравнению, называется рекуррентной последовательностью.
Объяснение:
ответ: у*(3/7+2/3+1-2/5)=у*(3/7+2/3+3/5)=у*(3*15+2*35+3*21)/105=у*173/105=у*1 68/105.
Объяснение: