1. Яке з поданих чисел ділиться на 2, але не ділиться на 5 ? А) 2540; Б) 3825; В) 7384; Г) 6220.
2. Яке число треба поставити замість * у виразі 53*21, щоб утворилось число, яке ділиться на 9 ?
А) 1; Б) 4; В) 7; Г) 9.
3. Виберіть найбільший дріб
А) ; Б) ; В) ; Г) .
4. У якій парі числа взаємно обернені?
А) 7 і ; Б) і ; В) і ; Г) і .
5. Яке з даних чисел є значенням виразу ?
А) ; Б) ; В) ; Г) .
6. Для чисел a, b, c, dпозначених на малюнку, записано нерівності. Яка з них хибна ?
a b c d
А) a В) b>c; Г) d>a.
Достатній рівень
7. Знайти значенням виразу
8.Яке з чисел дорівнює сумі –3+2+(–5)+6 ?
9.Чому дорівнює сума виразів 3k+2n–1і –4k–2n+2?
Високий рівень
10.Знайти частку коренів рівняння 2x–5–6x=11 i –5x+7=13?
11. Який із виразів після винесення за дужки перетворюється на вираз x∙(2y–3a+4)?
12. Що дістанемо, розкривши дужки і звівши подібні доданки у виразі–3 ∙ (x–2a) – 6a?
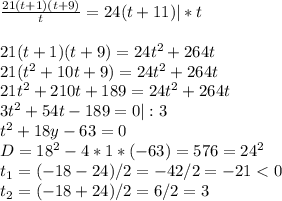
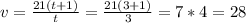(км/ч)
Пусть скорость третьего велосипедиста равна v км/ч,
а t ч - время, за которое он догнал второго велосипедиста.
До встречи третий и второй велосипедисты проехали одно и то же расстояние.
По условию задачи, второй ехал на 1 час больше, чем третий.
Тогда t+1 ч - время второго
Получаем:
Скорость (км/ч) Время (ч) Расстояние (км)
третий v t v*t
второй 21 t+1 21*(t+1)
Составляем первое уравнение: vt=21(t+1)
До встречи первый и третий проехали одинаковое расстояние, третий догнал первого через t+9 часов,
а первый на тот момент уже был в пути t+2+9=t+11 часов, т.к. выехал на 2 часа раньше третьего.
Получаем:
Скорость (км/ч) Время (ч) Расстояние (км)
третий v t+9 v*(t+9)
второй 24 t+11 24*(t+11)
Составляем второе уравнение: v(t+9)=24(t+11)
Решаем систему уравнений:
{ vt=21(t+1) => v=21(t+1)/t (подставим во второе уравнение)
{ v(t+9)=24(t+11)
Итак, t=3 часа
Находим скорость третьего велосипедиста:
ответ: 28 км/ч