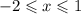
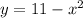
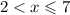
(3х - 2)(х - 3) = 20
3x² - 9x - 2x + 6 - 20 = 0
3x² - 11x - 14 = 0
D = (-11)² - 4 * 3 * (-14) = 121 + 168 = 289 = 17²
x1 = (11 + 17) / 6 = 28 / 6 = 14 / 3 = 4 целых 2/3
х2 = (11 - 17) / 6 = -1
ответ: 4 целых 2/3 или -1
(8х - 9)(3х + 2) - (2х - 3)(8х - 2) = 33х + 20
24х² + 16х - 27х -18 - 16x² + 4x + 24x - 6 - 33x - 20 = 0
8x² - 16x - 44 = 0 | : 4
2x² - 4x - 11 = 0
D = 16 + 88 = 104 = (2 √26)²
x1 = (4 + 2√26) / 4 = (2(2 + √26)) / 4 = (2 + √26) / 2
x2 = (4 - 2√26) / 4 = (2(2 - √26)) / 4 = (2 - √26) / 2
ответ : (2 + √26) / 2 или (2 - √26) / 2
(3х - 2)(х - 3) = 20
3x² - 9x - 2x + 6 - 20 = 0
3x² - 11x - 14 = 0
D = (-11)² - 4 * 3 * (-14) = 121 + 168 = 289 = 17²
x1 = (11 + 17) / 6 = 28 / 6 = 14 / 3 = 4 целых 2/3
х2 = (11 - 17) / 6 = -1
ответ: 4 целых 2/3 или -1
(8х - 9)(3х + 2) - (2х - 3)(8х - 2) = 33х + 20
24х² + 16х - 27х -18 - 16x² + 4x + 24x - 6 - 33x - 20 = 0
8x² - 16x - 44 = 0 | : 4
2x² - 4x - 11 = 0
D = 16 + 88 = 104 = (2 √26)²
x1 = (4 + 2√26) / 4 = (2(2 + √26)) / 4 = (2 + √26) / 2
x2 = (4 - 2√26) / 4 = (2(2 - √26)) / 4 = (2 - √26) / 2
ответ : (2 + √26) / 2 или (2 - √26) / 2
1. Если угловой коэффициент к положителен, линейная функция возрастает. если отрицателен, то убывает. в 1) к=2>0 ; во 2) k=4>0, значит, обе функции возрастают.
второй Используя свойства верных числовых неравенств, докажем, что возрастают функции
1) у = 9 + 2 х
Пусть х₁>х₂, у₁ = 9 + 2 х₁; у₂ = 9 + 2 х₂; тогда 2х₁>2х₂, т.к. умножали на положительное одно и то же число 2, 9+2х₁>9+2х₂, т.к. к обеим частям добалили одно и то же число 9, вывод у₁>у₂, доказано.
2) у = - 8 + 4х
аналогично
Пусть х₁>х₂, у₁ = -8+4х₁; у₂ = -8+4х₂; тогда 4х₁>4х₂, т.к. умножали на положительное одно и то же число 4; -8+4х₁>-8+4х₂, т.к. к обеим частям добалили одно и то же число -8, вывод у₁>у₂, доказано.
2. 1) свои наибольшее и наименьшее значения линейная функция достигает на концах отрезка. т.е. наименьшее равно у(-2)= 1.5-2*6=
-10.5; наибольшее у(1)=1.5+6=7.5
2) квадратичная функция у(7)=11-49=-38-наименьшее значение на указанном отрезке.