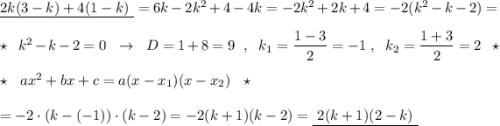
2k(3-k) + 4(1-k)
раскроем скобки.
1. 2k(3-k)=2к*3-2к*к=6к-2к²
2. 4(1-k)=4-4к
3. 2k(3-k) + 4(1-k)=6к-2к²+4-4к=-2к²+2к+4=-2*(к²-к-2)
Разложим на линейные множители квадратный трехчлен в скобках.
для этого решим квадратное уравнение. т.е. найдем корни квадратного трехчлена. к²-к-2=0; к=(1±√(1+8))/2=(1±3)/2; к=2; к=-1.
Квадратный трехчлен раскладываем на множители к²-к-2=(к-2)(к+1), собирая все, что получили раньше, имеем:
2k(3-k) + 4(1-k)=-2*(к-2)(к+1)=2*(2-к)*(к+1)=2*(k+1)(2-k).
Возведём обе части в квадрат:
(√(2x-20) + √(x+15))² = 25
Теперь всё раскрываем:
2x - 20 + 2√((2x-20)(x+15)) + x + 15 = 25
Теперь всё кроме корня перенесём вправо с противоположным знаком и вновь возведём в квадрат:
2√((2x-20)(x+15)) = 30 - 3x
4√((2x-20)(x+15))² = (30 - 3x)²
4(2x-20)(x+15) = (30 - 3x)²
4(2x² + 30x - 20x - 300) = 900 - 180x + 9x²
8x² + 120x - 80x - 1200 = 900 - 180x + 9x²
-x² + 220x - 2100 = 0
x² - 220x + 2100 = 0
x1 = 210; x2 = 10
Теперь попытаемся подставнокой проверить, какой корень будет удовлетворять уравнению:
В решении.
Объяснение:
Решить систему уравнений:
7x+2y=3
4x+3y= -2
Разделить второе уравнение (все части) на 4 для упрощения:
7x+2y=3
х+0,75у= -0,5
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
х= -0,5-0,75у
7( -0,5-0,75у)+2у=3
-3,5-5,25у+2у=3
-3,25у=3+3,5
-3,25у=6,5
у=6,5/-3,25
у= -2
х= -0,5-0,75у
х= -0,5 -0,75*(-2)
х= -0,5+1,5
х=1.
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.