Невозможно.
Объяснение:
Можно решить..
разложим на множители каждое из знаменателей:
x2 – 5x + 6 = x2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),
x2 – x – 2 = x2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),
x2 – 2x – 3 = x2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).
Следовательно Общий знаменатель равен (x – 3)(x – 2)(x + 1).
Теперь нам надо Умножить обе части уравнения. на общего знаменателя (x – 3) (x – 2) (x + 1) ,
3(x + 1) – 2(x – 3) = 2(x – 2) ,
3x + 3 – 2x + 6 = 2x – 4.
Следовательно
–x = –13 и x = 13.
63(x + 1) – 2(x – 3) = x – 2
3x + 3 – 2x + 6 = x – 2
3x – 2x – x = –3 – 6 – 2,
в таком случае можно было бы вполне получить
х=-11
Что в целом невозможно для последнего уравнения.
8
Объяснение:
Пусть все наши 14 карточек находится по порядку и не "склеиваются". Тогда поставим между ними знак + и посчитаем сумму
5 + 5 + 5 + … + 5 = 5*14 = 70 < 295 - не получилось.
Наша сумма оказалась слишком маленькая поэтому нам неоюходимо соединять карточки 5 в числа. Ясно, что в 555 соединять не надо - слишком много. Тогда попробуем по порядку:
1 число 55: 55 + 5 + 5 + ... + 5 = 115 < 295 - не попали
2 чисел 55: 55 + 55 + 5 + 5 + ... + 5 = 160 - снова не попали
3 числа 55: 55 + 55 + 55 + 5 + ... = 205 < 295 - опять не то
4 числа 55: 55 + 55 + 55 + 55 + 5 + ... = 250 < 295 - близко, но не то
5 чисел 55: 55 + 55 + 55 + 55 + 55 + 5 + 5 + 5 + 5 = 295 - Получилось!
Тогда посчитаем количество плюсов в примере
55 + 55 + 55 + 55 + 55 + 5 + 5 + 5 + 5
Получим 8 штук - и это ответ!
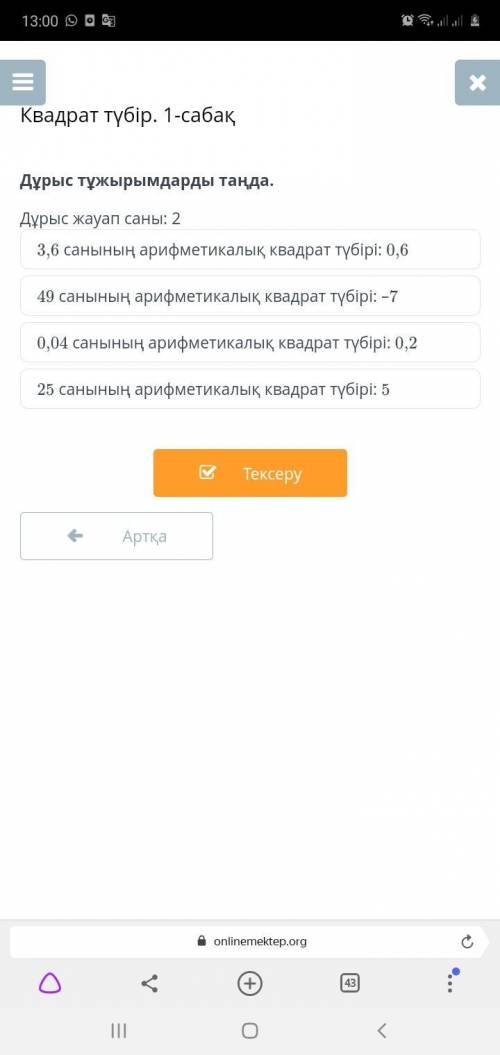
ответ:0.04 и 0.02. 25 и5
Объяснение:
100%