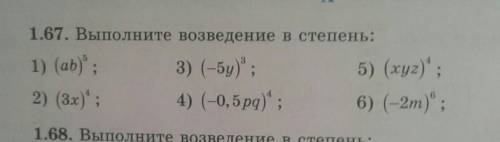
Вычислить площадь фигуры, ограниченной линиями
y=e^x, y=e^-x, x=1
поскольку обе кривые пересекаются в точке х=0 у=1
и не обращаются в ноль то
площадь фигуры, ограниченной линиями y=e^x, y=e^-x, x=1
равна площади фигуры, ограниченной линиями y=e^x у=0 x=0 x=1
минус площадь фигуры, ограниченной линиями y=e^-x у=0 x=0 x=1
первая это интеграл от нуля до 1 от e^x
вторая это интеграл от нуля до 1 от e^-x
интеграл от e^-x = - e^-x
остается подставить значения и найти каждый интеграл а затем из первого вычесть второй
Объяснение:
1)(ab)^5=a^5b^5
2) (3x)^4=3^4x^4=81x^4
3)(-5y)³=(-5)^3y³=-125y³
4)(-0,5pq)^4=(-0,5)^4p^4q^4=0,0625p^4q^4
5)(xyz)^4=x^4y^4z^4
6)(-2m)^6=(-2)^6m^6=64m^6