"Дана функция y=x2−4. Построй график функции y=x2−4.
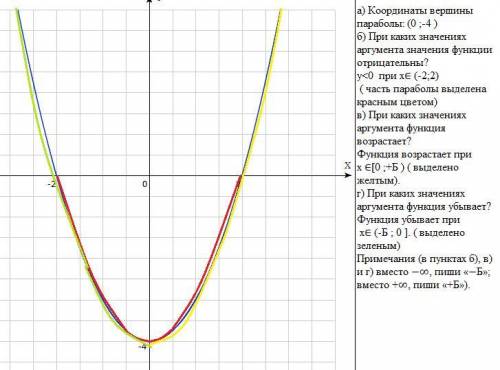
a) Координаты вершины параболы: ( ; )
(в пунктах б), в) и г) вместо −∞, пиши «−Б»; вместо +∞, пиши «+Б»).
б) При каких значениях аргумента значения функции отрицательны?
( ; ). в) При каких значениях аргумента функция возрастает? [ ; ).
г) При каких значениях аргумента функция убывает? ( ; ]
(Сравни свой график с представленным в шагах решения).
Объяснение:
a) Координаты вершины параболы: х₀=0/2=0 , у₀=0-4=-4 ; (0 ;-4 ) .
б) у<0 при х²-4<0
-------(+)------(-2)--------(-)--------(2)------(+) ,при х∈ (-2;2)
в) Функция возрастает при х≥0.
г) Функция убывает при х≤0.
дальше система:1 уравнение в системе) x>-5. берем значение х больше -5, пусть будет 0. подставляем.
0+5=5. значение получается больше нуля, следовательно знак модуля просто опускаем и переписываем все уравнение полностью без изменений.
2 уравнение в системе) x<=-5. берем значение х меньше -5. пусть будет -10. подставляем.
-10+5=-5. ответ получается меньше нуля. следовательно знак модуля убираем и у под модульного выражения меняем знак на противоположный. получается
-х-5>5х-7.
теперь приводишь подобные слагаемые.
должна получается система
x+5>5x-7 -4x>-12 x<3
-x-5>5x-7 -6x>-2 x<1/3
на оси координат находишь промежутки с учетом модулю, тоесть в первом уравнение x>-5, во втором x<=-5