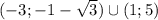Подайте у вигляді степеня добуток: 1. c•c•c•cc•c•c•c; 3. (-x) • (-x)•…•(-x); 2. 5b•5b•5b; 4. (a+b) • (a+b)•…•(a+b)

Подайте у вигляді степеня добуток: 1. c•c•c•cc•c•c•c; 3. (-x) • (-x)•…•(-x); 2. 5b•5b•5b; 4. (a+b) •

👇

Увидеть ответ

Открыть все ответы

Ответ:

Nessmikk13

27.12.2020

ОДЗ:

$\left \{ {{x^2+2x-20} \atop{ {x^2+2x-2\neq1 }\atop{\frac{|x+4|-|x|}{x-1}0 }} \right.$

Решаем каждое неравенство:

x^2+2x-20 ⇒ (x+1)^2-3 0 ⇒ $(x+1-\sqrt{3})(x+1+\sqrt{3})0$

$x\in (-\infty;-1-\sqrt{3}) \cup{-1+\sqrt{3};+\infty)$

$x^2+2x-2\neq 1$ ⇒ $x^2+2x-3\neq 0$ ⇒ $x\neq -3;$ $x\neq 1$

$\frac{|x+4|-|x|}{x-1}0$

Подмодульные выражения обращаются в 0 в точках

x=-4 и x=0

Это точки делят числовую прямую на три промежутка.

Раскрываем знак модуля на промежутках:

(-∞;-4]

|x+4|=-x-4

|x|=-x

$\frac{-x-4-(-x)}{x-1}0$ ⇒ $\frac{-4}{x-1}0$ ⇒ x < 1

решение неравенства (-∞;-4]

(-4;0]

|x+4|=x+4

|x|=-x

$\frac{x+4-(-x)}{x-1}0$ ⇒ $\frac{2x+4}{x-1}0$ ⇒ x < -2 или x > 1

решение неравенства (-4;-2)

(0;+∞)

|x+4|=x+4

|x|=x

$\frac{x+4-x}{x-1}0$ ⇒ $\frac{4}{x-1}0$ ⇒ x > 1

решение неравенства (1;+∞]

Объединяем ответы трех случаев:

$\frac{|x+4|-|x|}{x-1}0$ при $x \in (-\infty;-2)\cup(1;+\infty)$

ОДЗ:

$\left \{ {{x\in (-\infty;-1-\sqrt{3}) \cup{-1+\sqrt{3};+\infty)} \atop{ {x\neq-3; x\neq 1 }\atop{ x \in (-\infty;-2)\cup(1;+\infty)}} \right.$

$x\in (-\infty;-3)\cup(-3;1-\sqrt{3}) \cup(1;+\infty)$

Решаем неравенство: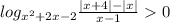 $log_{x^2+2x-2}\frac{|x+4|-|x|}{x-1}0$

$0=log_{x^2+2x-1}1$

$log_{x^2+2x-2}\frac{|x+4|-|x|}{x-1}log_{x^2+2x-2}1$

Два случая:

если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента

$\left \{ {{x^2+2x-21} \atop {\frac{|x+4|-|x|}{x-1}1}} \right.$ ⇒ $\left \{ {{x^2+2x-30} \atop {\frac{|x+4|-|x|-x+1}{x-1}0}} \right.$ ⇒ $\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.$

второе неравенство решаем на промежутках так:

(-∞;-4]

$\frac{-x-4-(-x)-x+1}{x-1}0$ ⇒ $\frac{-3-x}{x-1}0$ ⇒ $\frac{x+3}{x-1}$ ⇒ (-3;-1)

не принадлежат (-∞;-4]

на (-4;0]

$\frac{x+4-(-x)-x+1}{x-1}0$ ⇒ $\frac{x+5}{x-1}0$ ⇒ x < -5 или x > 1

не принадлежат (-4;0]

(0;+∞)

$\frac{x+4-x-x+1}{x-1}0$ ⇒ $\frac{5-x}{x-1}0$ ⇒ $\frac{x-5}{x-1}$ ⇒ $x\in (1;5)$

о т в е т этого случая (1;5)

если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента

$\left \{ {{0$ ⇒ $\left \{ {0$ ⇒ $\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.$

второе неравенство решаем на промежутках так:

(-∞;-4]

$\frac{-x-4-(-x)-x+1}{x-1}$ ⇒ $\frac{-3-x}{x-1}$ ⇒ $\frac{x+3}{x-1}0$ ⇒

(-∞;-3)U(1;+∞)

о т в е т. (-∞;-4]

на (-4;0]

$\frac{x+4-(-x)-x+1}{x-1}$ ⇒ $\frac{x+5}{x-1}$ ⇒ -5 < x < 1

о т в е т. (-4;0]

(0;+∞)

$\frac{x+4-x-x+1}{x-1}$ ⇒ $\frac{5-x}{x-1}$ ⇒ $\frac{x-5}{x-1}0$ ⇒ $x\in (0;1)\cup(5;+\infty)$

о т в е т этого случая $(-3;-1-\sqrt{3})$

С учетом ОДЗ получаем окончательный ответ: $(-3;-1-\sqrt{3})\cup(1;5)$

4,6(75 оценок)

Ответ:

GFGFDGDF

27.12.2020

(a + b)⁴ = а⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

Объяснение:

(a + b)⁴ = ((a + b)²)² = (a² + 2ab + b²)² = ...

Теперь можно многочлен умножить на многочлен.

А можно воспользоваться формулой (а+b+c)² = a² + b² + c² + 2ab + 2ac + 2bc.

Я сначала выполню обычное умножение, затем использую формулу, а Вы выбирайте удобный для Вас

(a + b)⁴ = ((a + b)²)² = (a² + 2ab + b²)² = (a² + 2ab + b²)•(a² + 2ab + b²) = а⁴ + 2а³b + a²b² + 2а³b + 4a²b² + 2ab³ + a²b² + 2ab³ + b⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

Или

(a + b)⁴ = ((a + b)²)² = (a² + 2ab + b²)² = а⁴ + 4а²b² + b⁴ + 4a³b + 2a²b² + 4ab³ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

4,7(7 оценок)

Это интересно:

Здоровье

27.06.2020

Как понизить артериальное давление быстро и эффективно?...

Компьютеры-и-электроника

21.05.2022

Как восстановить игру League Of Legends: шаг за шагом...

Хобби-и-рукоделие

23.06.2021