Здесь от каждой дроби берётся целая часть.
Значит, дроби меньше единицы здесь имеют целую часть, равную нулю:
![$\left[\frac{7}{10}\right]=0;\ \ \ \left[\frac{8}{10}\right]=0;\ \ \ \left[\frac{9}{10}\right]=0](/tpl/images/2010/2141/944b3.png)
Все остальные дроби (с числителями от 10 до 19)- каждая имеет целую часть, равную единице:![$\left[\frac{10}{10}\right]=\left[\frac{11}{10}\right]=\left[\frac{12}{10}\right]=\left[\frac{13}{10}\right]=\left[\frac{14}{10}\right]=\left[\frac{15}{10}\right]=\left[\frac{16}{10}\right]=\left[\frac{17}{10}\right]=\left[\frac{18}{10}\right]=\left[\frac{19}{10}\right]=1](/tpl/images/2010/2141/5a665.png)
Всего таких дробей 10 штук, что даст общую сумму всего примера, равную:
1 * 10 = 10
Или вот, полностью весь пример:![$\left[\frac{7}{10}\right]+\left[\frac{8}{10}\right]+\left[\frac{9}{10}\right]+\left[\frac{10}{10}\right]+\left[\frac{11}{10}\right]+\left[\frac{12}{10}\right]+\left[\frac{13}{10}\right]+\left[\frac{14}{10}\right]+\left[\frac{15}{10}\right]+\left[\frac{16}{10}\right]+\left[\frac{17}{10}\right]+\left[\frac{18}{10}\right]+\left[\frac{19}{10}\right]=](/tpl/images/2010/2141/0fa71.png)
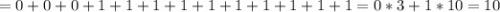
ответ: 10
P.S.
Целая часть находится делением нацело на 10
Например:
7 : 10 = 0 целых (и 7 в остатке)
10 : 10 = 1 целая (и 0 в остатке)
19 : 10 = 1 целая (и 9 в остатке)
Если бы был знаменатель посложнее, чем 10, то можно было бы делить уголком например. Ну, или на калькуляторе всегда можно поделить и увидеть целую часть дроби.
площадь прямоугольного треугольника равна половине произведения его катетов, поэтому нам надо найти катеты треугольника. если известен периметр 30 см и гипотенуза. то сумма двух катетов равна 30 - 13 = 17 (см).
пусть один катет равен х см, тогда второй катет равен (17 - х) см. по теореме пифагора составим уравнение и решим его.
13^2 = x^2 + (17 - x)^2 - раскроем скобку по формуле квадрата разности двух выражений;
169 = x^2 + 289 - 34x + x^2;
2x^2 - 34x + 120 = 0 - поделим почленно на 2;
x^2 - 17x + 60 = 0;
d = b^2 - 4ac;
d = (- 17)^2 - 4 * 1 * 60 = 289 - 240 = 49; √d = 7;
x = (- b ± √d)/(2a)
x1 = (17 + 7)/2 = 24/2 = 12 (см) - длина первого катета, 17 - 12 = 5 (см) - длина второго катета;
x2 = (17 - 7)/2 = 10/2 = 5 (см) - длина первого катета, 17 - 5 = 12 (см) - длина второго катета.
s = 1/2 * 12 * 5 = 6 * 5 = 30 (см^2).
ответ. 30 см^2.