Решите неравенства: 2x^2-13x+19 меньше или равно (x-3)^2 7x^2+12x+3 больше или равно (3x-1)*(3x+5) 1/(x+2) - id13888020210526 от danilaandriyanov 26.05.2021 23:42

Question

Алгебра: Решите неравенства: 2x^2-13x+19 меньше или равно (x-3)^2 7x^2+12x+3 больше или равно (3x-1)*(3x+5) 1/(x+2) больше или равно 1

danilaandriyanov · Accepted Answer

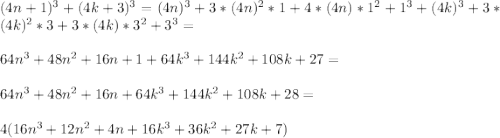
1. Здесь в условии опечатка, скорее всего в точке x₀ = -1.

Прямая y=x-2 касается графика функции y=f(x) в точке x₀ = -1, то эта точка является общей для обеих функций, тогда f(-1) = -1-2=-3

ответ: -3.

2. Производная функции 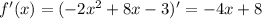f'(x)=(-2x^2+8x-3)'=-4x+8

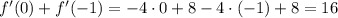
$f'(0)+f'(-1)=-4\cdot0+8-4\cdot(-1)+8=16$

ответ: 16.

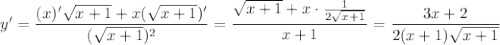
3. $y'=\dfrac{(x)'\sqrt{x+1}+x(\sqrt{x+1})'}{(\sqrt{x+1})^2}=\dfrac{\sqrt{x+1}+x\cdot\frac{1}{2\sqrt{x+1}}}{x+1}=\dfrac{3x+2}{2(x+1)\sqrt{x+1}}$

4. Производная функции: f'(x)=(2x^3-5x)'=6x^2-5

Используем геометрический смысл производной: f'(x₀) = tgα

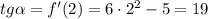
$tg\alpha=f'(2)=6\cdot2^2-5=19$

ответ: 19.

5. $f'(x)=(x^2-1)'(x^2+1)+(x^2-1)(x^2+1)'=2x(x^2+1)+2x(x^2-1)=\\ \\ =2x^3+2x+2x^3-2x=4x^3$

6. f(x)=(1-2x)(2x+1)=(1-2x)(1+2x)=1-4x^2

Производная функции: 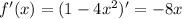f'(x)=(1-4x^2)'=-8x . Производная функции в точке 1, равна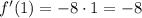 $f'(1)=-8\cdot1=-8$

7. Производная функции: f'(x) = 1/2√x, ее значение в точке х=1 равна 1/2. Тогда касательная: y = f'(x0)(x-x0) + f(x0) = 1/2 * (x-1) + 1 = x/2 + 1/2

y(31) = 31/2 + 1/2 = 32/2 = 16

ответ: 16.

8. $f'(x)=(x^2)'+(\sqrt{x})'=2x+\dfrac{1}{2\sqrt{x}}$

Решите неравенства: 2x^2-13x+19 меньше или равно (x-3)^2 7x^2+12x+3 больше или равно (3x-1)*(3x+5) 1/(x+2) больше или равно 1