ответ:1)Алгебраической называют дробью.
2)Тождество — это уравнение, которое удовлетворяется тождественно
3)число n (показывающее сколько раз повторяется множитель) – показателем степени
4)Квадратное уравнение называют приведенным, если его старший коэффициент равен 1.
5)Решить уравнение - значит найти все его корни или установить, что их нет.
6)Деление числителя и знаменателя на их общий делитель, отличный от
единицы, называют сокращением дроби.
7)при умножении ( делении ) числителя и знаменателя на одно и то же выражение ( число) получившаяся дробь = исходной
8)числители перемножаются отдельно
отдельно знаменатели
полученную дробь если это возможно сокращают
пример
2/3* 3/4 = (2*3)/(3*4)=6/12=1/2 (произвели сокращение на 6
9)Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
10) Сложение и вычитание алгебраических дробей c одинаковыми
знаменателями выполняется по тому же правилу, что и с обыкновенными
дробями:
аd + bd – cd = a+b−cd .
11) Нам известно, что дробь 34 равна частному 3 : 4 ,
значит, выражение ( 14+ 15) : ( 13− 16) = ( 14+ 15)( 13− 16) .
Частное двух чисел или выражений, в котором знак деления
обозначен чертой, называют дробным выражением.
Найдем значения выражений:
а) ( 14+ 15)( 13− 16) = ( 520+ 420)( 26− 16) = ( 920)( 16) = 920 : 16 =
= 920• 61 = 5420 = 2 710 = 2,7
12)Пусть a0 и a1 - натуральные числа. Для нахождения их наибольшего общего делителя используется алгоритм Евклида [1] последовательного деления с остатком: a0=a0a1+a2, a1=a1a2+a3, a2=a2a3+a4, … ,где натуральные числа a0,a1,a2, … суть неполные частные. Это алгоритм разложения числа a =a0/a1 в правильную цепную дробь, и он применим к любым вещественным числам a. При этомa0=[a], где [a] - целая часть числа a, a1=[1/(a-a0)], … , т.е.
a=a0+ 1a1+ 1a2+ 1a3+ ···,
13)http://school.xvatit.com/images/9/92/11-06-34.jpg
14)Складываются показатели степеней при УМНОЖЕНИИ степеней с одинаковыми основаниями.
2^3+2^5=8+32=40.
Подробнее - на -
Объяснение:
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
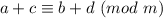
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
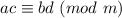
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
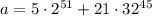
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,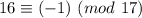 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что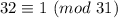 
, получаем
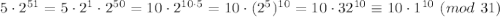
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
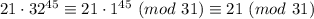
Остаток 21, чудесно. Выполняем последний шаг.
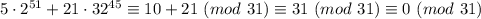
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
ответ: 1)
объяснение: так как
1*2*3*4=24