1)
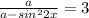
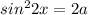
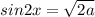
Так как значения синуса не могут быть большими единицы, получаем:
Так как выражение под радикалом и собственно весь радикал не могут быть отрицательными получаем:
Откуда получаем:
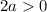
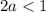
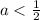
Объединяя полученные результаты получаем: a∈
ответ: a∈
2)
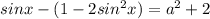
Получаем квадратное уравнение относительно t:
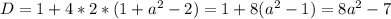
Исходя из того что данное уравнение должно иметь лишь одно решение получаем, что дискриминант должен быть равен нулю:
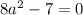
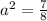
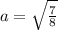
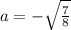
Но так как нам нужно только одно решение в заданном промежутке получаем:
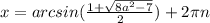
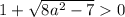
неравенство не имеет решений
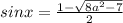
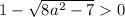
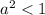
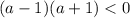
Получаем, что при a∈
данное уравнение имеет лишь один корень
ответ: a∈
Вероятность попадания в мишень одного стрелка при одном выстреле для первого стрелка равна 0.8, для второго стрелка – 0.85. Стрелки произвели по одному выстрелу в мишень. Считая попадание в цель для отдельных стрелков событиями независимыми, найти вероятность события А – ровно одно попадание в цель.
Решение.
Рассмотрим событие A - одно попадание в цель. Возможные варианты наступления этого события следующие:
Попал первый стрелок, второй стрелок промахнулся: P(A/H1)=p1*(1-p2)=0.8*(1-0.85)=0.12
Первый стрелок промахнулся, второй стрелок попал в мишень: P(A/H2)=(1-p1)*p2=(1-0.8)*0.85=0.17
Первый и второй стрелки независимо друг от друга попали в мишень: P(A/H1H2)=p1*p2=0.8*0.85=0.68
Тогда вероятность события А – ровно одно попадание в цель, будет равна: P(A) = 0.12+0.17+0.68 = 0.97
Объяснение:
ответ:с(с-1)
Объяснение: И в уменьшаемом,и в вычитаемом есть С. Выносим за скобки,С в квадрате=с×с,следовательно с(с-1). Вычитаемое С=с×1.