Пусть 
(км/ч) - первоначальная скорость мотоциклиста.
Тогда время, за которое он преодолел путь в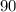 
километров, равно 
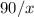часов.
Но, с другой стороны, сумма трех других отрезков времени равна тому же промежутку времени (по условию). Это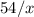 
часов, 
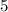минут или же 
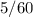часа = 
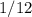часа. И последний промежуток, 
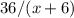часов (
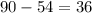километров со скоростью 
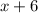км/ч).
Теперь, конечно, будем решать уравнение:
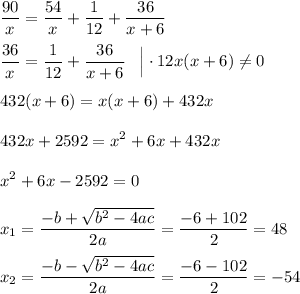
Получилось два корня. Второй доверия не внушает из-за своей отрицательности, так что возьмем исключительно первый.
Первоначальная скорость мотоциклиста -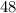 
км/ч.
Задача решена!
ответ: 48 км / ч .
а) 17 + x > 37
x > 37 - 17
x > 20
б) 5 - x ≤ 1
-x ≤ 1 - 5
-x ≤ -4
x ≥ 4
в) 6,2 + x ≥ 10
x ≥ 10 - 6,2
x ≥ 3,8
г) 0,6 - 2x < 0
-2x < -0,6
x > 0,3
2.
а) 1 + 6x < 7
6x < 6
x < 1
б) 6x + 1 > 0
6x > -1
x > -1/6
в) 3 - 2x ≤ 8
-2x ≤ 5
x ≥ -2,5
г) 6 - 15x ≥ 0
-15x ≥ -6
x ≤ 6/15
x ≤ 2/5
3.
а) 4 + x < 1 - 2x
x + 2x < 1 - 4
3x < -3
x < -1
б) 2 + 6x > 5 + 7x
6x - 7x > 3
-x > 3
x < -3
в) 4x + 7 ≤ 6x + 1
4x - 6x ≤ -6
x ≥ 3
г) 9x ≥ 4x + 2
5x ≥ 2
x ≥ 0,4
4.
a) 4(1+x) > x - 2
4 + 4x > x - 2
3x > -6
x > -2
б) -(2x - 1) ≤ 3(x + 2)
-2x + 1 ≤ 3x + 6
-5x ≤ 5
x ≥ -1
в) 6(2x - 1) - (2 + x) < 0
12x - 6 - 2 - x < 0
11x < 8
x < 8/11
г) 4(1 - x) + 5(x + 8) ≥ 0
4 - 4x + 5x + 40 ≥ 0
x ≥ -44