Испытание состоит в том, что два раза подряд бросают игральный кубик.
Число исходов испытания
n=6·6=36
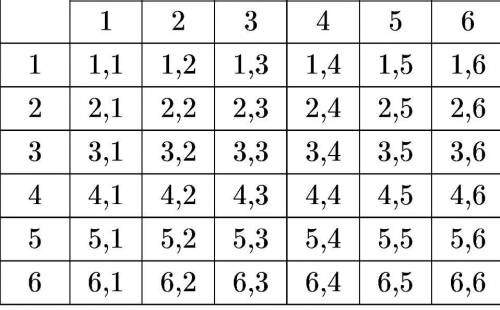
Результаты можно изобразить в виде таблицы:
( см. рис.1)
Первая цифра -число очков, выпавшее на первом кубике,
вторая цифра - число очков, выпавшее на первом кубике.
Получаем 36 двузначных чисел:
от 11 до 16; от 21 до 26; ... от 61 до 66.
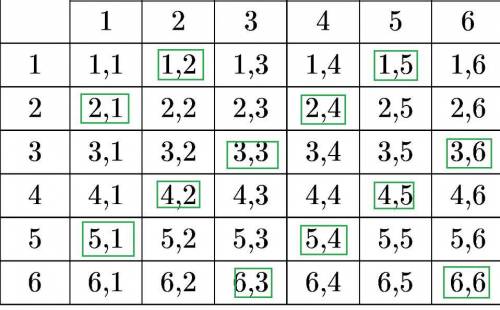
Событие A-"результатом двух последовательных бросков игрального кубика будет число, кратное трем"
m=12 ( cм. рис. 2)
это двузначные числа:
12;15; 21;24;33;36;42;45;51;54;63;66
По формуле классической вероятности
p(A)=m/n=12/36=1/3
1.Выражение не разложимо на множители на множестве рациональных чисел.
x²−2x+6
3.Выражение не разложимо на множители на множестве рациональных чисел.
3y²+6y−82
5.Множитель 1/2 выносим из каждого члена.
1/2(2а²+a+62)
7.Разложим многочлен на множители.
1/2⋅(2x²−a+62)
9.Выражение не разложимо на множители на множестве рациональных чисел.
3x²+2x+5
2.Выражение не разложимо на множители на множестве рациональных чисел.
4b²+2b−11
4.Множитель 1212 выносим из каждого члена.
1/2(p²+10p−16)
6.Множитель 1414 выносим из каждого члена.
1/4(c²+4c−24)
8.Выражение не разложимо на множители на множестве рациональных чисел.
2x²+4x−7
k²-9m²= (k-3m)(k+3m)
81x²-y²=(9x-y)(9x+y)
27x+3y=3(9x+y)
d²-4d+4=(d-2)^2
6d-12=6(d-2)
2a-2=2(a-1)
a²-2a+1=(a-1)^2
x²+8xy+16y²=(x+4y)^2
3x+12y=3(x+4y)