
Объяснение:
1. Уравнение вида a·x=b, где x – переменная, a и b – некоторые числа, называется линейным уравнением с одной переменной
Линейное уравнение - это алгебраическое уравнение, в котором все неизвестные имеют степень не более первой, и отсутствуют произведения неизвестных
2. Корнем (или решением) линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство
Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.
3. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных.
Решение системы уравнений — это последовательность чисел (k1, k2, ..., kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2, ..., xn дает верное числовое равенство.
4. Решить систему уравнений — это значит найти все её решения или установить, что решений нет.
1 ) (x-1)(x+2)=0
x-1 = 0 ; x + 2 = 0 ;
x = 1 ; x = -2
2) (2a+7)(a-5) = 0
2a + 7 = 0 ; a - 5 = 0;
a = -7/2 = -3,5 ; a = 5 ;
3) -3x(0,4x-12)=0
-3x = 0 ; 0,4x-12=0;
x =0 ; x = 30
4) (3x-5)(x+3)(x-4)=0
3x-5 =0 ; x +3 =0 ; x -4 =0
x = 5/3 ; x = -3 ;x =4
5) 5x(x+1)(3x-19) = 0
5x = 0 ; x+1 = 0 ; 3x-19 = 0
x = 0 ; x = -1 ; x =19/3;
6)x^4 = 0
x = 0
7) (2+3x)^2=0
2 + 3x =0 ;
x = -2/3;
8) x^2 - 4x = 0
x(x-4) = 0
x = 0 ; x = 4 ;
9) x^3-3x^2 = 0 ;
x^2(x-3)=0
x = 0 ; x = 3 ;
10) z^2-9=0
z = 3 ;
11) x^3 - 4x = 0
x(x^2-4) = 0
x = 0 ; x = 2 ; x = -2
12) x^2 + 4x + 4 = 0
D = 16 - 16 = 0 ;
x = 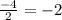
во вложении
Объяснение:
Алгебраическая дробь не имеет смысла, тогда, когда в знаменателе находится 0,т.к на ноль делить нельзя.
В решении возле каждого примеры написаны значения, которые в знаменателе дают ноль