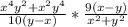при x=-7 и ОЧЕНЬ
Уравнение здесь имеет вид u3+u=v3+v, где u=2x2, v=3x+5a. От него можно перейти к равносильному равенству u=v по следующей причине. Функция f(u)=u3+u имеет производную f′(u)=3u2+1, которая всюду положительна. Поэтому f(u) строго монотонно возрастает на всей области определения. Поэтому её значения в различных точках не могут совпадать. Таким образом, мы приходим к равносильному условию u=v, а это квадратное уравнение 2x2−3x−5a=0. Находим дискриминант, и пишем, что он положителен: в этом и только в этом случае уравнение будет иметь более одного корня.
Объяснение:
x^2*y^2*(x^2+y^2)*9(x-y) / -10(x-y)*(x^2+y^2)=9x^2*y^2 /-10=
9*(-7)^2*(1/7)^2 /-10=-9/10 (^- значок степени)