Question

(Хотя бы один пример , просто чтобы понять как это делать)

Answer 1

Відповідь:$\sqrt[3]{а}$

Пояснення:

Answer 2

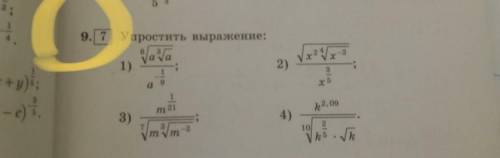
Объяснение:

$1) \ \frac{\sqrt[6]{a*\sqrt[3]{a} } }{a^{-\frac{1}{9}}} =\frac{\sqrt[6]{a}*\sqrt[18]{a} }{a^{-\frac{1}{9}} }=a^{\frac{1}{6}}*a^{\frac{1}{1 8}}*a^{\frac{1}{9}}=a^{\frac{1 }{6}+\frac{1}{18}+\frac{1}{9} }=a^{\frac{3+1+2}{18} }=a^{\frac{6}{18}}=a^{\frac{1}{3}}=\sqrt[3]{a}.\\$

$2)\ \frac{\sqrt{x^2*\sqrt[4]{x^{-2}} } }{x^{\frac{3}{5} }} =\frac{x*\sqrt[8]{x^{-2}} }{x^{0,6}} =x*x^{-0,25}*x^{-0,6}=x^{0,15}=\sqrt[20]{x^3}.\\ 3)\ \frac{m^{\frac{1}{21} }}{\sqrt[7]{m*\sqrt[3]{m^{-2}} } } =\frac{m^{\frac{1}{21} }}{\sqrt[7]{m}*\sqrt[21]{m^{-2}} }=m^{\frac{1}{21}}*m^{-\frac{1}{7} }*m^{\frac{2}{21} } =m^{\frac{1}{21}-\frac{1}{7}+\frac{2}{21}}=\\=m^{\frac{1-3+2}{21}}=m^{ \frac{0}{21} }=m^0=1}.$

$4)\ \frac{k^{2,09}}{\sqrt[10]{k^{\frac{2}{5}}*\sqrt{k} } } =\frac{k^{2,09}}{\sqrt[10]{k^{0,4}*k^{0,5} } } =\frac{k^{2,09}}{\sqrt[10]{k^{0,9}} } =\frac{k^{2,09}}{k^{0,09}}=k^{2,09-0,09}=k^2.$