ответ: 2) 2 является правильным ответом.
ответ:1. Вспомним формулы сокращенного умножения.
В нашем выражении присутствует вторая степень. Значит, можно воспользоваться формулами сокращенного умножения со второй степенью:
квадрат суммы: (a + b)^2 = a^2 + 2ab + b^2;
квадрат разности: (a - b)^2 = a^2 - 2ab + b^2;
разность квадратов: a^2 - b^2 = (a - b)*(a + b).
2. Выделим квадрат разности.
Проанализировав выражение, увидим, что 4а^2 - 20аb + 25b^2 похоже на квадрат разности. Определим значения для a и b.
4а^2 - 20аb + 25b^2 = (2a)^2 - 2*(2a)*(5b) + (5b)^2 = (2a - 5b)^2.
Подставим полученный квадрат разности в первоначальное выражение.
(2a - 5b)^2 - 36.
3. Разложим на множители.
Заметим, что 36 = 6^2. Подставим это в выражение.
(2a - 5b)^2 - 6^2.
Теперь мы имеем разность квадратов, где a = 2a - 5b, b = 6.
Подставим эти значения в формулу сокращенного умножения вместо a и b:
((2a - 5b) - 6)*((2a - 5b) + 6);
(2a - 5b - 6)*(2a - 5b + 6).
Следовательно, 4а^2 - 20аb + 25b^2 - 36 = (2a - 5b - 6)*(2a - 5b + 6).
Объяснение:
Объяснение:
1) Положим, существует такое число, которое может выразиться несократимой дробью 
, при этом p - целое, q - натуральное, которое удовлетворяет соотношению:
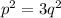
Из этого следует, что p², и p делятся на 3. Тогда p можно представить как 3c, тогда уравнение перепишется в виде:
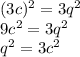
Отсюда следует, что и q делится на 3, а это противоречит условию несократимости дроби изначально. Следовательно на множестве рациональных чисел решений нет.
2) UPD: решается так же, немного не тот путь указал.
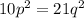
p² и p делятся на 21, значит p представимо в виде p = 21c
Тогда:
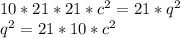
Стало быть, q тоже делится на 21, условие о несократимости дроби p/q нарушена, и значит решений нет на рациональном множестве
‥・Здравствуйте, teleprod07! ・‥
• ответ:
Правильным ответом к задаче «1. Какое из чисел является решением неравенства 3х > х+3?» является ответ под цифрой 2. (Оно же 2) 2.)
• Как и почему?
Для того, чтобы нам найти правильность моего ответа, то мы должны размышлять логически по плану, который будет представлен ниже:
1. Если мы в неравенство 3х > х+3 подставим вместо х число -1, то неравенство будет ложным: 3×-1 > -1+3 = Ложь.
2. Если мы в неравенство 3х > х+3 подставим вместо х число 0, то неравенство, естественно, тоже будет ложным. Я думаю, что это нам и так понятно, т.к.: 3×0 > 0+3 = Ложь.
3. Если мы в неравенство 3х > х+3 подставим вместо х число -2, то неравенство опять будет ложным: 3×-2 > -2+3 = Ложь.
4. А если же мы в неравенство 3х > х+3 подставим вместо х число 2, то уже неравенство будет истинным: 3×2 > 2+3 = Истина, т.к. 3 умножить на 2 будет 6, а к 2 прибавить 3 будет 5. 6 же у нас больше, чем 5, значит, берём вместо х число 2.
〔 P. S. : Не забываем такое правило, что если у нас между какими-то цифрами или буквами нет никакого знака, то это значит, что мы должны умножать их. 〕
‥・С уважением, Ваша GraceMiller! :) ・‥