b+bq+bq^2+bq^3+bq^4+bq^5 = b*(1+q+q^2+q^3+q^4+q^5) = 364,5*(1+(8/9)+(8/9)^2+(8/9)^3+(8/9)^4+(8/9)^5) = 1662+53/162 = 1662,32716 сумма первых шести ее членов
Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность это обозначает, что оставшаяся последовательность будет сходящейся в обоих случаях и ее предел равен 8
Обозначим друзей 1, 2, 3, 4, 5. 1 может взять любую шляпу из 2, 3, 4, 5 - всего 4 варианта. Допустим, 1 взял шляпу 2. Тогда 2 может взять любую из 1, 3, 4, 5. Если 2 берет шляпу 1, то для 3, 4 и 5 остаются шляпы 3, 4, 5. Они могут взять каждый чужую шляпу такими или 534. Если 2 берет шляпу 3, то для 3, 4, 5 остаются шляпы 1, 4, 5. Они могут взять каждый чужую шляпу такими Если 2 берет шляпу 4, то для 3, 4, 5 остаются шляпы 1, 3, 5. Они могут взять каждый чужую шляпу такими Если 2 берет шляпу 5, то для 3, 4, 5 остаются шляпы 1, 3, 4. Они могут взять каждый чужую шляпу такими Всего 11 вариантов, если 1 берет шляпу 2. Точно такие же варианты будут, если 1 возьмет шляпу 3, 4 или 5. Только надо поменять местами эту шляпу со шляпой 2. Поэтому всего получается 4*11 = 44 варианта.
ответ: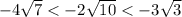 .
.
Объяснение: