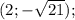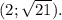Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом - задаются тригонометрическими формулами. А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
y² - 3y + 9 = 0
-5x² - 3 = 8x
4t + 2t² - 5 = 0
Полное квадратное уравнение имеет вид: ax² + bx + c = 0
1) y² - 3y + 9 = 0 (подходит)
уравнение совпадает с его стандартным видом и не является неполным
2) 37 - 4p² = 0 (не подходит)
-4p² + 37 = 0
уравнение не совпадает с его стандартным видом и является полным
3) z² + 6z = -3z (не подходит)
z² + 6z - 3z = 0
z² + 3z = 0
уравнение не совпадает с его стандартным видом и является полным
4) -5x² - 3 = 8x (подходит)
-5x² + 8x - 3 = 0
уравнение совпадает с его стандартным видом и не является неполным
5) 4t + 2t² - 5 = 0 (подходит)
2t² + 4t - 5 = 0
уравнение совпадает с его стандартным видом и не является неполным
а)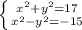
Сложим:
Подставим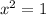 в первое уравнение:
в первое уравнение:
ответы: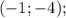
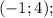
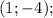
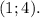
б)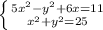
Сложим:
1)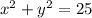 при
при 
2)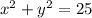 =>
=>  ₂ = 2
₂ = 2
2² + y² = 25
y² = 25 - 4
y² = 21
y₁ = - √21
y₂ = √21
ответы: