37. Найдите координаты вершины параболы 1) y = x² – 7x + 10; 2) y = -x² + x + 2;
3) y = -x² + 6x – 9;
4) y = x² + 4x + 5.

Question

Алгебра: 37. Найдите координаты вершины параболы 1) y = x² – 7x + 10; 2) y = -x² + x + 2; 3) y = -x² + 6x – 9; 4) y = x² + 4x + 5.​

Laki333 · Accepted Answer

При делении получится некоторый многочлен степени n:

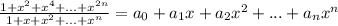
$\frac{1+x^2+x^4+...+x^{2n}}{1+x+x^2+...+x^n}=a_0+a_1x+a_2x^2+...+a_nx^n$

Избавимся от знаменателя:

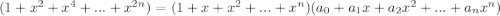
$(1+x^2+x^4+...+x^{2n})=(1+x+x^2+...+x^n)(a_0+a_1x+a_2x^2+...+a_nx^n)$

Раскроем скобки в правой части:

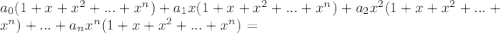
a_0(1+x+x^2+...+x^n)+a_1x(1+x+x^2+...+x^n)+ a_2x^2(1+x+x^2+...+x^n)+...+ a_nx^n(1+x+x^2+...+x^n)=

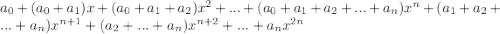
$a_0+(a_0+a_1)x+(a_0+a_1+a_2)x^2+...+(a_0+a_1+a_2+...+a_n)x^n+(a_1+a_2+...+a_n)x^{n+1}+(a_2+...+a_n)x^{n+2}+...+a_nx^{2n}$

Коэффициенты при нечётных степенях должны быть равны нулю, а коэффициенты при чётных степенях должны быть равны 1:

a_0=1

a_0+a_1=0

a_0+a_1+a_2=1

...

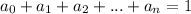a_0+a_1+a_2+...+a_n=1 , при чётном n

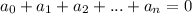a_0+a_1+a_2+...+a_n=0 , при нечётном n

...

a_n=1

Отсюда получаем, что 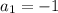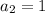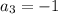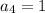a_1=-1 , a_2=1 , a_3=-1 , a_4=1 , и так далее, коэффициенты с нечётными индексами равны -1, а коэффициенты с чётными индексами равны 1.

Так как a_n=1, то очевидно, что n должно быть чётным, при этом при любом чётном n будут существовать корректные наборы коэффициентов a_i.

ответ: при любом чётном n.

37. Найдите координаты вершины параболы 1) y = x² – 7x + 10; 2) y = -x² + x + 2;3) y = -x² + 6x – 9;4) y = x² + 4x + 5.​

MOGZ ответил

37. Найдите координаты вершины параболы 1) y = x² – 7x + 10; 2) y = -x² + x + 2;
3) y = -x² + 6x – 9;
4) y = x² + 4x + 5.