(см. объяснение)
Объяснение:
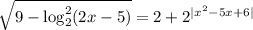
Введем функции 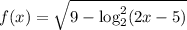 и
и  . Про вторую сразу скажем, что
. Про вторую сразу скажем, что 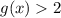 , но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это
, но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это 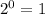 при
при 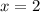 или
или 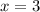 . Тогда наименьшее значение этой функции будет равно
. Тогда наименьшее значение этой функции будет равно 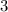 .
.
Теперь разберемся с 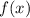 . У нас есть квадратный корень, поэтому все значения функции точно
. У нас есть квадратный корень, поэтому все значения функции точно 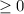 . Но и здесь мы идем дальше. Поменяем временно
. Но и здесь мы идем дальше. Поменяем временно 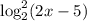 на букву
на букву 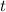 . Тогда будет
. Тогда будет 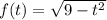 . Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное
. Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное 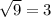 при
при 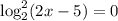 , откуда
, откуда 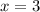 .
.
Наибольшее значение 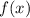 равно
равно 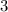 и достигается при
и достигается при 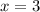 . Наименьшее значение
. Наименьшее значение 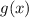 равно
равно 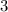 и достигается при
и достигается при 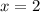 или
или 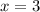 .
.
Тогда единственный корень исходного уравнения 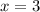 .
.
Уравнение решено!
в x^3+3*x-5.
Результат: y=-5. Точка: (0, -5)Точки пересечения графика функции с осью координат X:График функции пересекает ось X при y=0, значит нам надо решить уравнение:x^3+3*x-5 = 0 Решаем это уравнение и его корни будут точками пересечения с X:
x=-(-5/2 + sqrt(29)/2)**(1/3) + (-5/2 + sqrt(29)/2)**(-1/3)≈1,15417. Точка: (1,15417, 0)Экстремумы функции:Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:y'=3*x^2 + 3=0
Решаем это уравнение и его корни будут экстремумами:
x = √-1 - нет решения и нет экстремумов.
Точки перегибов графика функции:Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции,
+ нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции:y''=6*x=0
Решаем это уравнение и его корни будут точками, где у графика перегибы:x=0. Точка: (0, -5)Интервалы выпуклости, вогнутости:Найдем интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках изгибов:Вогнутая на промежутках: [0, oo)Выпуклая на промежутках: (-oo, 0]Вертикальные асимптоты графика функции:Горизонтальную асимптоту найдем с предела данной функции при x->+oo и x->-oo. Соотвествующие пределы находим :lim x^3+3*x-5, x->+oo = oo, значит горизонтальной асимптоты справа не существуетlim x^3+3*x-5, x->-oo = -oo, значит горизонтальной асимптоты слева не существуетНаклонные асимптоты графика функции:Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы :lim x^3+3*x-5/x, x->+oo = oo, значит наклонной асимптоты справа не существуетlim x^3+3*x-5/x, x->-oo = oo, значит наклонной асимптоты слева не существуетЧетность и нечетность функции:Проверим функци четна или нечетна с соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем:x^3+3*x-5 = -x^3 - 3*x - 5 - Нетx^3+3*x-5 = -(-x^3 - 3*x - 5) - Нетзначит, функция не является ни четной ни нечетной