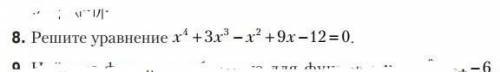
Для начала найдем угловой коэффициент этой прямой.
Точки A и B задают прямоугольный треугольник с катетами 3 и 4.
угловой коэффициент - это тангенс угла это прямой к оси x.
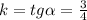
с другой стороны угловой коэффициент - это производная от g(x)
Выходят две точки, т.к. это с гиперболой две точки касания одних и тех же прямых, с одинаковым коэффициентом.
Но нам даны точки через которые проходит прямая.
Легче всего схематично построить графики прямой и g(x). Увивдим что подходит положительное значение, т.е. x=2.
ответ: x=2
-4 ; 1
Объяснение:
х⁴ +3х³-х²+9х-12=0
x⁴-x²+3x³+9x-12=0
x²(x²-1)+3(x³+3x-4)=0
x²(x²-1)+3(x³-x+4x-4)=0
x²(x²-1)+3(x(x²-1)+4(x-1))=0
x²(x²-1)+3(x(x-1)(x+1)+4(x-1))=0
x²(x-1)(x+1)+3(x-1)(x(x+1)+4)=0
x²(x-1)(x+1)+3(x-1)(x²+x+4)=0
(x-1)(x²(x+1)+3(x²+x+4))=0
(x-1)(x³+x²+3(x²+x+4))=0
(x-1)(x³+x²+3x²+3x+12)=0
(x-1)(x³+4x²+3x+12)=0
(x-1)(x²(x+4)+3(x+4))=0
(x-1)(x²+3)(x+4)=0
x-1=0
x=1
x²+3=0
x²= -3
x∈∅ в действительных решениях.
x+4=0
x= -4