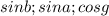
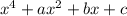 по условию он должен быть, квадратом некого многочлена.
по условию он должен быть, квадратом некого многочлена. 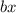 , а он не возможен при квадрате , и заметим то что старшая степень равна
, а он не возможен при квадрате , и заметим то что старшая степень равна 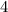 .
. 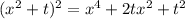 . Что есть частный случаи многочлена.
. Что есть частный случаи многочлена. 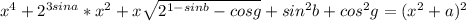
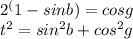
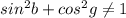 так как оно противоречит условию
так как оно противоречит условию 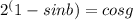 что не имеет решений.
что не имеет решений. 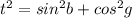
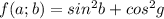 очевидно
очевидно 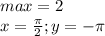 .
. 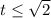 . Что согласуется с значение
. Что согласуется с значение 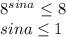 .
. 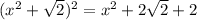
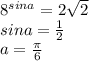
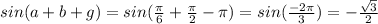
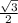
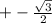
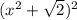
xU S T
по течениюx+2 40 вместе 3 T=S /U
против X-2 6
40/x+2 + 6/ x-2=3
40(x-2)+6(x+2)=3(x^2-4)
40x-80+6x+12=3(x^2-4)
46x-68=3(x^2-4)
46x-3x^2-68+12=0
-3^2x -56+46x=0
дискриминант а=-3 b=46 c=-56
D=46^2-4* -3*-56=2116-672=1444 >0 38
x1=-46-38/-6=14
x2=8/6
проверяем 14+2=16 40/16+6/12=2.5+0,5=3 часа (формула первая)
второе проверяем 8/6-2 короче его не бери оно полюбому не подойдет там даже отрицательное