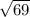
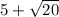
Область определения функции определится по условиям, что знаменатель не может быть нулем, а под корнем не должно быть отрицательное число.
а) 16x²-49<>0
(4x-7)(4x+7)<>0
4x<>7
x<>7/4
4x<>-7
x<>-7/4
x ∈ (-∞;-7/4)U(-7/4; 7/4)U(7/4; +∞)
y ∈ (-∞; +∞)
б) x²+4x+3>0
найдем корни
x²+4x+3 = 0
По теореме Виета
х1 = -3
х2 = -1
(x+3)(x+1)>0
x+3>0, x>-3
x+1>0, x>-1
x > -1
x+3<0, x<-3
x+1<0, x<-1
x < -3
x ∈ (-∞; -3]U[-1; +∞)
Поскольку подразумевается арифметический корень, то у ∈ [0; +∞)
6 * 6 = 36
Но нас устраивает только когда сумма двух выпавших чисел равна 6 и 9. Посчитаем количество благоприятных исходов:
Когда сумма 6:
1-5 ; 2-4 ; 3-3 ; 4-2 ; 5-1 = 5 исходов
Когда сумма 9:
6-3 ; 5-4 ; 4-5 ; 3-6 = 4 исхода
Вероятность находится - отношением благоприятных исходов к максимально возможным (благоприятные + неблагоприятные), т.е.
ответ: 0,25