Объяснение:
cos 175ͦ × ctg 300ͦ / sin 297ͦ × tg 135ͦ=
cos 175ͦ - знак "-" так как 175°- 2 четверть, а cos во 2 четверти
отрицателен
ctg 300ͦ - знак "-" так как 300°- 4 четверть, а ctg во 4 четверти
отрицателен
sin 297ͦ - знак "-" так как 297°- 4 четверть, а sin во 2 четверти
отрицателен
tg 135ͦ - знак "-" так как 135°- 2 четверть, а tg во 2 четверти
отрицателен
"-"*"-"/"-"*"-"= +
ответ: +
К сожалению, площадь дороги не указаны, поэтому решим задачу в общем виде.
Пусть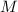 
- вместимость грузовика
Пусть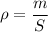 
, где 
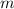- масса щебенки, необходимая на всю отсыпку дорог, 
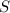- общая площадь дорог.
Наше количество грузовиков высчитаем по такой формуле:
![\displaystyle n=\left[\frac{m}{M}\right]+1](/tpl/images/1015/9278/1a699.png)
, то есть это общая масса щебенки, деленная на массу щебенки, влезающей в один грузовик, взятая от всего этого целая часть и плюс один. К примеру, общая масса 120 кг, вместимость грузовика 50кг, 120/50=2.4, [2.4]=2, 2+1=3, оно так и будет: в 2 грузовика по 50 кг и в 1 грузовик 20кг. Будет одно исключение, о котором позже.
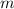не известно, выразим его через известные величины:
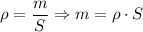
![\displaystyle n=\left[\frac{m}{M}\right]+1 \Rightarrow n=\left[\frac{\rho \cdot S}{M}\right]+1](/tpl/images/1015/9278/418e5.png)
Теперь подставим все чиселки, за исключением площади, которая должна быть в этой задаче, но куда-то пропала:
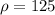кг/м²
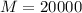кг/машина
![\displaystyle n=\left[\frac{125 \cdot S}{20000}\right]+1= \left[\frac{S}{32}\right]+1](/tpl/images/1015/9278/cd282.png)
Так вот исключением будет случай, когда S кратно 160 м², то есть когда в целой части будет целое число. В этом случае прибавлять лишний грузовик не надо (+1 делать), хотя по жизненной логике это наоборот хорошо, потому что предельно нагружать машины не стоит, так как в таких ситуациях всегда может произойти что-то плохое, но к данной задаче это отношения не имеет, поэтому надо учитывать данную особенность.
В решении.
Объяснение:
Между какими соседними натуральными числами заключено число: 1)√27 ≈ 5,2
Между 5 и 6.
2)√135-2 ≈ 11,6-2 ≈ 9,6
Между 9 и 10.
3)√14 ≈ 3,7
Между 3 и 4.
4)√321 ≈ 17,9
Между 17 и 18.
Для памятки:
Натуральные - это те, с которых выражают целое количество предметов - два яблока, три апельсина. То есть натуральные числа это умное название для привычных всем чисел 1, 2, 3, 4 и так далее.
Если к натуральным добавить ноль и отрицательные, то это будет называться целые числа.
А если добавить и дроби - то это рациональные числа.