y=x^2-3x+3,
y=-x^2+x+9
x^2-3x+3 = -x^2+x+9
2x^2-4x-6=0
x^2-2x-3=0
x1=-1 ; x2=3
S = S2 - S1 =
=∫(-x^2+x+9)dx - ∫(x^2-3x+3)dx =
= -x^3/3+x^2/2+9x |[-1;3] - x^3/3-3x^2/2+3x |[-1;3] =
=-3^3/3+3^2/2+9*3-[-(-1)^3/3+(-1)^2/2+9(-1)]-(3^3/3-3*3^2/2+3*3-[(-1)^3/3-3*(-1)^2/2+3*(-1)])=
=64/3
Войти
АнонимМатематика06 февраля 00:30
Решите систему уравнений: 3x² - 2x = y 3x - 2 = y
ответ или решение1
Осипова Алла
1) Подставим в первое уравнение системы значение у, взяв его из второго уравнения:
3х^2 - 2х = 3х - 2.
2) Перенесем члены из правой части в левую и приравняем значение выражения к 0:
3х^2 - 2х - 3х + 2 = 0;
3х^2 - 5х + 2 = 0.
3) Решим полученное квадратное уравнение:
D = (-5)^2 - 4 * 3 * 2 = 25 - 24 = 1.
D > 0, то уравнение имеет 2 корня:
х1 = (-(-5) + 1) / (2 * 3);
х1 = 1;
х2 = (-(-5) - 1) / (2 * 3);
х2 = 4/6;
х2 = 2/3.
4) Найдем значения у:
у1 = 3х1 - 2;
у1 = 3 * 1 - 2;
у1 = 1;
у2 = 3х2 - 2;
у2 = 3 * 2/3 - 2;
у2 = 0.
ответ: (1; 1); (2/3; 0).
Объяснение:
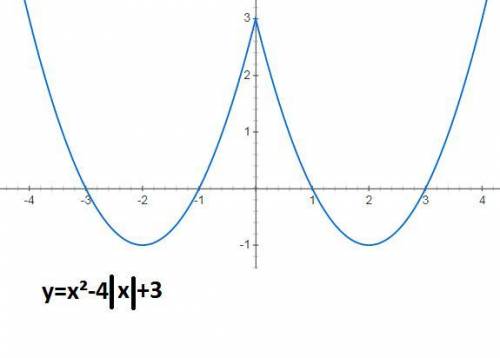
y=x²-4|x|+3 = Ix²I-4|x|+3
это четная функция y(-x)=y(x)
график четной функции симметричен относительно оси ОУ.
Можно построить график для х>0 f а затем симметрично отобразить его относительно оси ОУ
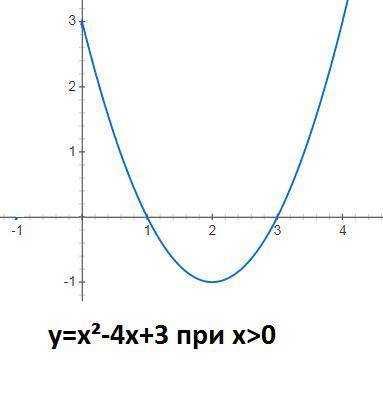
1) Построим график для х>0
при x>o IxI=x тогда y=x²-4|x|+3=x²-4x+3
y=x²-4x+3
это график квадратичной функции
вершина параболы х₀=-b/2a=4/2=2
y₀=y(2)=4-8+3=-1 (2;-1)
точка пересечения с осью ОУ х=0 у=3 (0;3)
точки пересечения с осью ОХ
у=0 x²-4x+3=0
x²-x-3x+3=x(x-1)-3(x-1)=(x-1)(x-3)=0
x₁=1 ; x2=3
(1;0) (3;0)
строим параболу при х>0
2) симметрично отображаем отображаем ее относительно оси ОУ
определим границы площади
y=x^2-3x+3,
y=-x^2+x+9
приравняем по у
x^2-3x+3 = -x^2+x+9
2x^2-4x-6=0
x^2-2x-3=0
x1=-1 ; x2=3
интервал [-1;3]
S = S2 - S1 =
=∫(-x^2+x+9)dx - ∫(x^2-3x+3)dx =
= -x^3/3+x^2/2+9x |[-1;3] - x^3/3-3x^2/2+3x |[-1;3] =
=-3^3/3+3^2/2+9*3-[-(-1)^3/3+(-1)^2/2+9(-1)]-(3^3/3-3*3^2/2+3*3-[(-1)^3/3-3*(-1)^2/2+3*(-1)])=
=64/3
ответ 64/3