Искомая функция 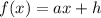 .
.
Найдем значения искомой функции в заданных точках х:
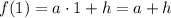
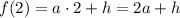
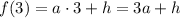
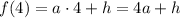
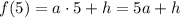
Кроме этого, для каждого из аргументов есть еще и экспериментальное значение, которое обозначим через функцию 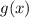 :
:
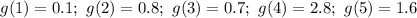
Составим функцию 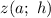 , которая будет суммировать квадраты разностей значений функций
, которая будет суммировать квадраты разностей значений функций  и
и  соответствующих аргументов:
соответствующих аргументов:
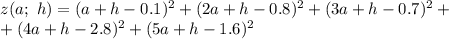
Исследуем эту функцию на экстремум.
Найдем частные производные:
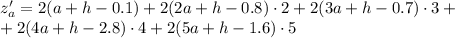
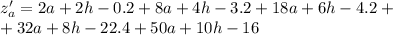
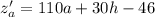
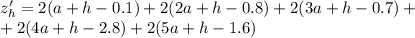
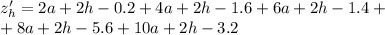
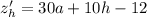
Необходимое условие экстремума: равенство нулю частных производных:
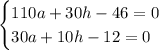
Домножим второе уравнение на (-3):
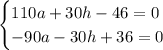
Складываем уравнения:
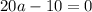
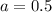
Подставим значение а во второе уравнение исходной системы:
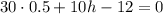
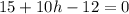
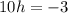

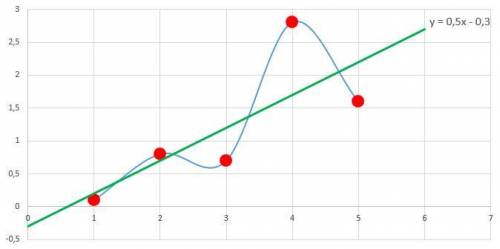
Точка (0.5; -0.3) - предполагаемая точка экстремума.
Найдем вторые частные производные функции:
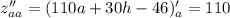
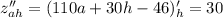
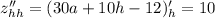
Рассмотрим выражение:

Так как 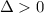 и
и 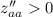 , то точка (0.5; -0.3) является точкой минимума.
, то точка (0.5; -0.3) является точкой минимума.
Значит, в точке (0.5; -0.3) функция 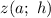 имеет минимум.
имеет минимум.
Тогда, значения 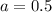 и
и  есть искомые коэффициенты функции
есть искомые коэффициенты функции 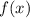 .
.
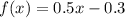
ответ: 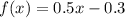
1) (1,75; 5,75)
2) (3; 3)
3) у = 7х
Объяснение:
Точкой пересечения графиков функций будет точка, (х,у), подходящая для обоих равенств.
То есть строго говоря это такая точка (х, у), где х и у являются решением системы уравнений:
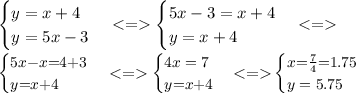
И искомые координаты точки будут (1,75; 5,75)
Можно решить проще:
Чтобы найти абсциссу (х) точки пересечения, приравняем

А ординату (у) точки пересечения найдем, подставив найденное значение (х) в любое из уравнений:
Например, в y = x + 4
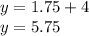
И искомые координаты точки будут (1,75; 5,75)
ответ (1,75; 5,75)
2.
Найти точку графика, абсцисса которой равна ординате

То есть требуется найти такую точку (х,у) графика,
у которой х = у.
Строго говоря, тут также требуется решение системы:
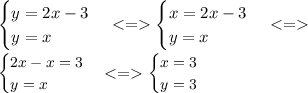
Это как бы пересечение двух графиков:
у = 2х - 3 и у = х
Но можно и проще.
Найти точку графика, абсцисса которой равна ординате, т.е. у = х.
Значит, подставляем х вместо у в уравнение;
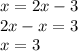
А так как по условию у = х, то

И искомые координаты точки будут (3; 3)
ответ: (3; 3)
3.
График линейной функции проходит через начало координат (т.е. точку О(0; 0)) и точку А(3; 21)
Следовательно, уравнение имеет форму
y = kx + b
причем т.к. график проходит через (0;0), следовательно
у(0) = 0 => 0 = k•0 + b <=> b = 0
а значит уравнение прямой имеет форму:
y = kx + 0 <=> y = kx
И т.к. график проходит через А(3; 21), следовательно
у(3) = 21 <=> k•3 = 21 <=> k = 21:3
k = 7
Итак, получили, что b = 0; k = 7
А значит уравнение примет вид:
у = 7х
ответ: у = 7х
Областью определения прямой служит множество значений обратной функции. и наоборот.