Question

1/х +1/(х+4) = 5/24 разберите полностью как решать(

Answer 1

$\frac{1}{x}+\frac{1}{(x+4)}=\frac{5}{24}$

$\frac{2(x+2)}{x(x+4)}=\frac{5}{24}$

$x=-\frac{12}{5}$

$x=8$

Answer 2

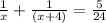
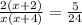
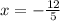
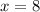
1/х +1/(х+4) = 5/24

ОДЗ: х не равен 0, иначе знаменатель дроби 1/х обращается в ноль.

          х не равен -4, иначе  знаменатель дроби 1/(х+4) обращается в ноль.

Приведем дроби к общему знаменателю: х(х+1), получим:

(х+4+х)/(х)(х+4)=5/24

Избавляемся от знаменателей

5*(х)(х+4) = 24(2х+4)

5(х²+4х)=48х+96

5х²+20х=48х+96

5х²-28х-96=0

D= 784+1920=2704

х1=(28-52)/10 = -2,4

х2=(28+52)/10=8

т. к.оба корня удовлетворяют ОДЗ, значит, являются решением уравнения.

ответ: х=-2,4, х=8.