Признак сходимости знакочередующихся рядов (признак Лейбница):
Пусть имеется ряд
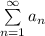
Тогда, если выполнены условия:
Ряд является знакочередующимся. Члены ряда убывают по модулю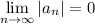
то ряд сходится.
1) Чередование знаков
Ряд является знакочередующимся, т.к. присутствует множитель 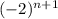
2) Убывание по модулю
![\lim\limits_{n\to \infty}|\frac{(-2)^{n+1}}{2+3^n} |=\lim\limits_{n\to \infty}\frac{2^{n+1}}{2+3^n}=[\frac{\infty}{\infty} ]](/tpl/images/2004/2358/902ef.png)
Неопределенность вида "бесконечность делить на бесконечность" решим по правилу Лопиталя
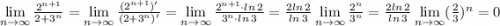
Таким образом, ряд сходится
Тип сходимости Сходящийся ряд 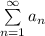 называют абсолютно сходящимся, если сходится ряд
называют абсолютно сходящимся, если сходится ряд 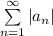 .
.
Сходимость такого ряда можно определить с предельного признака Даламбера
![\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|} =\lim\limits_{n\to \infty}\frac{2^{n+2}}{2+3^{n+1}}:\frac{2^{n+1}}{2+3^{n}} =\lim\limits_{n\to \infty}\frac{2^{n+2}}{2+3^{n+1}}\cdot\frac{2+3^{n}}{2^{n+1}} =2\lim\limits_{n\to \infty}\frac{2+3^{n}}{2+3^{n+1}}=[\frac{\infty}{\infty} ]](/tpl/images/2004/2358/41dfd.png)
Неопределенность вида "бесконечность делить на бесконечность" решим по правилу Лопиталя
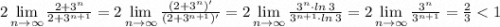
Ряд сходится по признаку Вейерштрасса, следовательно исходный ряд сходится абсолютно.
Объяснение:
cos(π/3+x) - 0,5√3cos(x-π) = -1/4
По формулам:
cos(π/3+x) = cos(π/3)*cos x - sin(π/3)*sin x = 1/2*cos x - √3/2*sin x
0,5√3*cos(x-π) = √3/2*(-cos x) = -√3/2*cos x
Подставляем в уравнение
1/2*cos x - √3/2*sin x + √3/2*cos x = -1/4
Умножаем всё на 4 и переносим 1/4 налево
2cos x - 2√3*sin x + 2√3*cos x + 1 = 0
(2+2√3)*cos x - 2√3*sin x + 1 = 0
Переводим всё в половинный аргумент
(2+2√3)(cos^2(x/2) - sin^2(x/2)) - 2√3*2sin(x/2)*cos(x/2) + cos^2(x/2) + sin^2(x/2) = 0
(2+2√3+1)*cos^2(x/2) - 4√3*sin(x/2)*cos(x/2) + (1-2-2√3)*sin^2(x/2) = 0
Делим всё на cos^2(x/2)
(3+2√3) - 4√3*tg(x/2) + (-1-2√3)*tg^2(x/2) = 0
Замена tg (x/2) = y. Получаем квадратное уравнение.
Умножаем всё на -1
(1+2√3)*y^2 + 4√3*y - (3+2√3) = 0
D/4 = (2√3)^2 + (1+2√3)(3+2√3) = 4*3 + (3+8√3+12) = 27 + 8√3
Далее решаем и получаем ответ.
Писать это все у меня сейчас времени нет.
Потом
x = 2arctg(y)