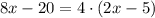
В решении.
Объяснение:
Дана функция у=√х:
а) График которой проходит через точку с координатами А(а; 4). Найдите значение а.
Нужно в уравнение подставить известные значения х и у (координаты точки А):
4 = √а
(4)² = (√а)²
16 = а
а=16;
б) График функции проходит через точку М(36; m). Найдите значение m.
Нужно в уравнение подставить известные значения х и у (координаты точки А):
m = √36
m = 6;
в) Если х∈[0; 25], то какие значения будет принимать данная функция?
у= √х
у=√0=0;
у=√25=5;
При х∈ [0; 25] у∈ [0; 5].
г) y∈ [13; 19]. Найдите значение аргумента.
13 = √х
(13)² = (√х)²
х=169;
19 = √х
(19)² = (√х)²
х=361;
При х∈ [169; 361] y∈ [13; 19].
Объяснение:
Нужно решить полное квадратное уравнение 2x2 + 5x - 7 = 0.
И насколько нам известно мы должны вспомнить и вычислить дискриминант первым действием.
D = b2 - 4ac;
Начнем с того, что выпишем коэффициенты уравнения:
a = 2; b = 5; c = -7;
Вычисляем дискриминант:
D = 52 - 4 * 2 * (-7) = 25 + 56 = 81;
Корни уравнения мы ищем по следующим формулам:
x1 = (-b + √D)/2a = (-5 + √81)/4 = (-5 + 9)/4 = 4/4 = 1;
x2 = (-b - √D)/2a = (-5 - √81)/4 = (-5 - 9)/4 = -14/4 = -3,5;
ответ: x = 1 и x = -3,5 корни уравнения