1)5
2)4
вроде бы так,у меня тоже было такое
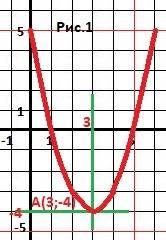
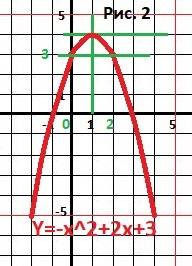
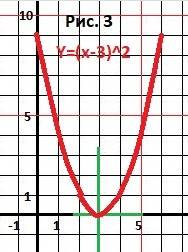
Объяснение:
Находим границы фигуры, приравняв функции:
x² - 4 = -x - 2.
Получаем квадратное уравнение х²+ х - 2 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=1^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√9-1)/(2*1)=(3-1)/2=2/2=1;x_2=(-√9-1)/(2*1)=(-3-1)/2=-4/2=-2.
Искомая площадь фигуры равна интегралу:
S= \int\limits^1_{-2} {(-x-2- x^{2} +4} \, dx = \int\limits^1_{-2} {(- x^{2} -x+2)} \, dx =- \frac{x^3}{3}- \frac{ x^{2} }{2}+2x|_{-2}^1S=−2∫1(−x−2−x2+4dx=−2∫1(−x2−x+2)dx=−3x3−2x2+2x∣−21
Подставив пределы, получаем: S =((-1/3)-(1/2)+2*1) - ((8/3)-4/2+2*(-2)) =
= (7/6)-(-10/3) = 9/2 = 4,