Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что , то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что (при этом подразумевая, что )
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: )
Возможно, это не очень явно, поэтому вспомним, что по предположению , и доделаем:
А это прямо яркий пример противоречия: предположив, что , мы получили .
Из этого следует, что , но и из предположенного же уже следует, что .
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что (при этом )
И тогда уже точно исходя из пунктов 1) и 2), получаем
Поскольку коэффициент при икс квадрат не равен 0, то перед нами -квадратное уравнение. Наличие и кол-во корней определяются дескреминантом. если D<0 -корней нет если D=0 - 1 корень если D>0 - 2 корня Чтобы были корни, как требует наше условие диксриминант модет быть либо равен нулю либо больше 0, а именно: D≥0 решения на самом деле 2 1) находим все t при которых отрицательный диксриминант (не имеет корней уравнение) и удаляем это промежуток из интервала (-беск:+беск) 2) находим все t при которых D≥0 Воспользуемся D=4t^2-36t≥0 4t(t-9)≥0 t∈(-inf;0)u(9:+inf)
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что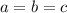 , то есть
, то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что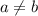 (при этом подразумевая, что
(при этом подразумевая, что 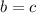 )
)
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: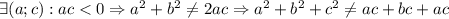 )
)
Возможно, это не очень явно, поэтому вспомним, что по предположению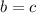 , и доделаем:
, и доделаем:
А это прямо яркий пример противоречия: предположив, что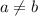 , мы получили
, мы получили 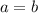 .
.
Из этого следует, что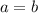 , но и из предположенного же
, но и из предположенного же 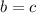 уже следует, что
уже следует, что 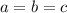 .
.
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что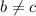 (при этом
(при этом 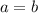 )
)
И тогда уже точно исходя из пунктов 1) и 2), получаем