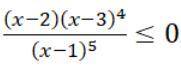
1.Ix-2I+Ix+3I=2-x+x+3=5
2. ((2x-3)³)¹/³-2x=2x-3-2x=-3
3. (x²+y²-x²-xy)*(x/y)/(x*(x¹/²+y¹/²))=(y²-yx)/(y**(x¹/²+y¹/²))=
y*(x¹/²+y¹/²)(x¹/²-y¹/²)/(y**(x¹/²+y¹/²))=)(x¹/²-y¹/²)=√x-√y;
√0.09-√0.04=03-0.2=01;
4. 5х²+9х+64=64; 5х²+9х=0; х*(5х+9)=0; х=0; х=-1.8
сумма корней 0-1.8=-1.8
6. ОДЗ х²+3х-18>0; По Виету корни уравнения х²+3х-18=0
это х=-6 и х=3
-63
+ - +
х∈(-∞;-6)∪(3;+∞)
т.к. 4 меньше 9 при любом х из ОДЗ, то ответ х∈(-∞;-6)∪(3;+∞)
5. отнимем от первого уравнения второе . получим 6∛у=6, откуда у=1, тогда 2∛х=-7+3, ∛х=-2, х=-8
ответ (-8;1)
Объяснение:
1)5(2а + 1) – 3=10а+5-3 =10а+2
4) (х-6)^2-2х(-3х-6)=х²-12х+36+6х²+12х=7х²+36
5. Решите уравнение:
5у+2(3-4у)=2у+2
5у+6-8у=2у+2
5у-8у-2у=2-6
-5у=-4
у=-4:(-5)
у=0,8
6) Пусть боковая сторона х см, тогда основание будет (Х+8) см. Так периметр равен 44 см, составим и решим уравнение
х+х+х+8=44
3х+8=44
3х=44-8
3х=36
х=36:3
х=12
12+8=20
ответ: 12 см; 12 см; 20 см;
8) Из второго уравнения 4х – 6у = 0⇒2х-3у=0⇒2х=3у Подставим в 1 уравнение 3у+3у=-12 ⇒6у=-12⇒у=-12:6⇒у=-2
Тогда 2х+3·(-2)=-12⇒2х-6=-12⇒2х=-12+6⇒2х=-6⇒х=-6:2⇒х=-3
Отает: (-3;-2) или х=-3; у=-2
У нет заданий: 2,3,7;
Объяснение:
Найдем нули функции (нули числителя) и особые точки (нули знаменателя):
числитель:
- закрашенные точки на оси
знаменатель:
- выколотая точка на оси
Отметим точки на оси, определим знаки на интервалах и выделим область