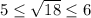
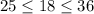
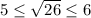 . Возведя все части неравенства в квадрат, получим
. Возведя все части неравенства в квадрат, получим 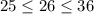 . Неравенства выполняются, следовательно, число √26 заключен между числа 5 и 6.
. Неравенства выполняются, следовательно, число √26 заключен между числа 5 и 6.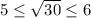 . Возведя все части неравенства в квадрат, получим:
. Возведя все части неравенства в квадрат, получим: 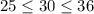 . Видим, что неравенства правильны, следовательно, число √30 заключен между числа 5 и 6.
. Видим, что неравенства правильны, следовательно, число √30 заключен между числа 5 и 6.3. Прямоугольность треугольника проверяется по формуле
c²=a²+b² (c>b>a)
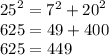
Так как 625≠449, ΔKMP не прямоугольный
6. Высота равнобедренного треугольника находится по формуле
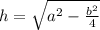
где h — высота, a — боковая сторона, b — основание
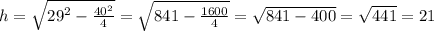
высота треугольника равна 21 см
9. По теореме Пифагора (теорема Пифагора гласит, что сумма квадратов катетов равна квадрату гипотенузы): c²=a²+b²
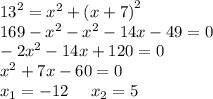
Так как длина не может быть отрицательной a=5, b=5+7=12
Площадь прямоугольного треугольника находится по формуле:
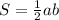
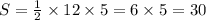
Площадь треугольника равен 30 см²
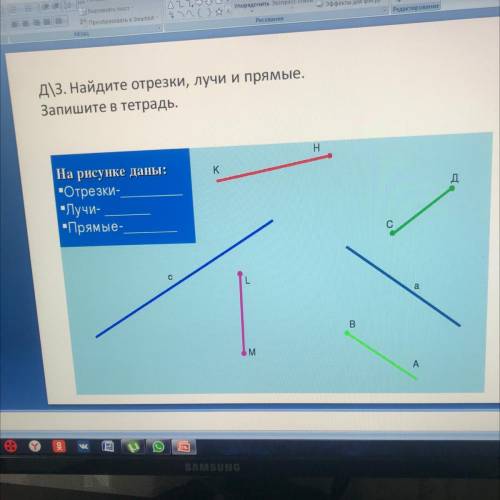
КН-луч
С-прямая
LM-отрезок
ВА-луч
А-прямая
СД-отрезок