
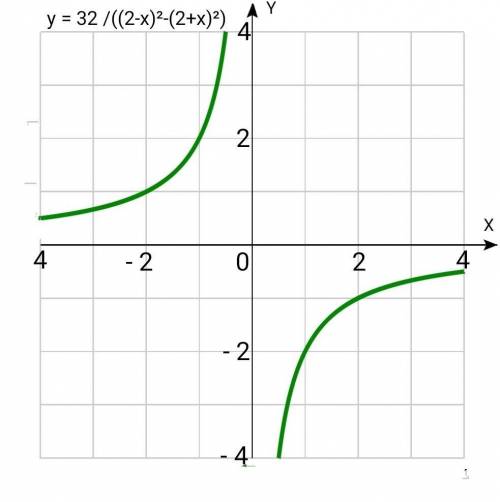
график в прикреплённом изображении.
Объяснение:
у = 32 /((2-х)²-(2+х)²)
1.
Найдём область определения функции:
выражение, записанное в знаменателе дроби, отлично от нуля,
(2-х)²-(2+х)² ≠ 0
(2-х+2+х)(2-х-2-х) ≠ 0
4•(-2х) ≠ 0
-8х ≠ 0
х ≠ 0
хє(-∞;0) ∪ (0; +∞)
2.
у = 32 /((2-х)²-(2+х)²)
у = 32 /(-8х)
у = - 4/х - обратная пропорциональность, графиком является гипербола.
Составим таблицу значений, отметим точки с указанными координатами, соединив их, получим ветви гиперболы:
х l 1 l 2 l 4 l 8 l
y l -4 l -2 l -1 l - 1/2l
Вторая ветвь гиперболы с точками, координаты которых симметричны относительно начала координат.
80*80/x-80=80*180/(80-x)-180
8*(80/x-1)=18*(80/(80-x)-1)
4*(80-x)/x=9*(80-80+x)/(80-x)
4*(80-x)/x=9x/(80-x)
4*(80-x)^2=9x^2
4*(6400-160x+x^2)=9x^2
25600-640x+4x^2=9x^2
5x^2+640x-25600=0
x^2+128x-5120=0
D=36864=192^2x
х1=(-128-192)/2<0 - не подходит под условия задачи (расстояние не может быть отрицательным)
x2=(-128+192)/2=32
х=32
ответ: 32 км