я не поняла последний пример, нет правильно я всё оставляю дробью,если надо десятками дели сам

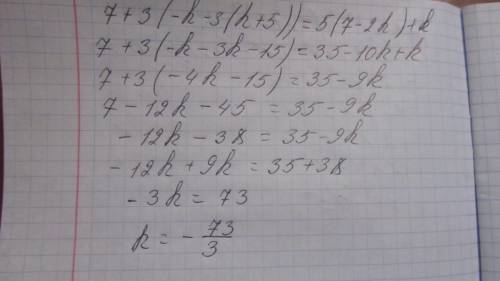
Луна — единственный естественный спутник Земли. Самый близкий к Солнцу спутник планеты, так как у ближайших к Солнцу планет (Меркурия и Венеры) их нет. Второй по яркости объект на земном небосводе после Солнца и пятый по величине естественный спутник планеты Солнечной системы.
Луна появилась около 4,51 млрд лет назад, немного позже Земли. Наиболее популярна гипотеза о том, что Луна сформировалась из осколков, оставшихся после «Гигантского столкновения» Земли и Тейи — планеты, схожей по размерам с Марсом.
Объяснение:
Задания на свойства и графики квадратичной функции вызывают, как показывает практика, серьезные затруднения. Это довольно странно, ибо квадратичную функцию проходят в 8 классе, а потом всю первую четверть 9-го класса "вымучивают" свойства параболы и строят ее графики для различных параметров.
Это связано с тем, что заставляя учащихся строить параболы, практически не уделяют времени на "чтение" графиков, то есть не практикуют осмысление информации, полученной с картинки. Видимо, предполагается, что, построив десятка два графиков, сообразительный школьник сам обнаружит и сформулирует связь коэффициентов в формуле и внешний вид графика. На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
Не будем требовать от школьников невозможного и предложим один из алгоритмов решения подобных задач.
Итак, функция вида y = ax2 + bx + c называется квадратичной, графиком ее является парабола. Как следует из названия, главным слагаемым является ax2. То есть а не должно равняться нулю, остальные коэффициенты (b и с) нулю равняться могут.
Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.
Самая зависимость для коэффициента а. Большинство школьников уверенно отвечает: " если а > 0, то ветви параболы направлены вверх, а если а < 0, – то вниз". Совершенно верно. Ниже приведен график квадратичной функции, у которой а > 0.
y = 0,5x2 - 3x + 1
В данном случае а = 0,5

А теперь для а < 0:
1) 3-6x-15+5x-18x+24=83
-19x=83-3+15-24
-19x=71
x=-3.73
2) 23-3b-3+30b-35-21b+7=0
6b=-23+3+35-7
6b=8
b=0.125
3) 2x(2)+3-5x(2)+15x=21x-3x(2)
-6x=-3
x=0.5
4) 2m+3m-m(2)-m=2m-m(2)+12
2m=12
m=6