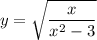
Знаменатель не должен равняться нолю, а подкоренное выражение должно быть не отрицательным. Условия для знаменателя будет учитываться при рассмотрении условия для выражения под корнем.

Разложим выражение в знаменателе на множители с формулы сокращённого умножения: a²-b² = (a-b)(a+b).
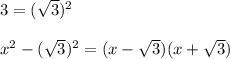
Тогда имеем:
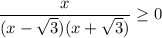
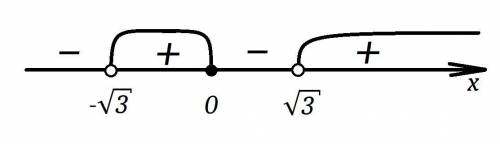
Решим неравенство с метода интервалов:
Отмечаем на координатной прямой точки, в которых выражения из числителя и знаменателя обращаются в ноль. И выкалываем те, что относятся к знаменателю (на ноль делить нельзя). Мы получили 4 интервала. Перед дробью знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда больше или равно нуля, поэтому выбираем интервалы с плюсом и учитываем их границы.
Получили:
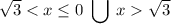
ответ: 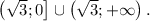
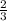
Объяснение:
У нас 6 резцов: 2 изношенных и 4 новых.
Производится 2 извлечения.
Нам нужно, чтобы во втором извлечении попался новый резец.
Рассмотрим все случаи:
1) при первом извлечении попался изношенный резец, значит шанс:
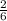 ;
;
осталось 5 резцов: 1 изношенный, 4 новых, значит шанс, что попадётся новый резец:
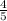 ;
;
всё это должно произойти одновременно, значит умножаем:
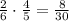 .
.
2) при первом извлечении попался новый резец, значит шанс:
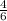 ;
;
осталось 5 резцов: 2 изношенных и 3 новых, значит шанс, что попадётся новый резец:

всё это должно произойти одновременно, значит умножаем:
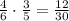 .
.
Может произойти любой из рассмотренных случаев, значит складываем:
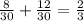
=lim(x⇒+∞) (1+2/x²+3/x³)/(5+3/x²-2/x³)=(1+0+0)/(5+0-0)=1/5=0,2.