Объяснение:
Для того чтобы показать, что число является составным достаточно показать, что оно у него есть делители помимо 1 и самого себя. Для начала надо понять на какое число заканчивается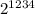 
. Для этого нужно понять на какую цифру заканчиваются степени двойки:
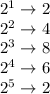
Таким образом последняя цифра в степенях двойки может быть только из множества {2, 4, 8, 6}, которое будет циклически повторяться. Дальше надо понять остаток от деления 1234 на 4. 1234 : 4 = 308 и остаток 2. Значит последния цифра у нас совершит 308 полных циклов и еще 2 шага. Таким образом число 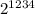заканчивается на цифру 4. Следовательно 
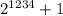заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
23.12.20 :: 13:04:19 Выбор языка:
Russian
Добро Гость выберите Вход или Регистрация
В ПАТЕНТОВАНИИ СТАТЬИ И ПУБЛИКАЦИИ Научно-техническая библиотекаНаучно-техническая библиотека SciTecLibrary Правила форума
Отправить
Научно-технический форум SciTecLibrary › Точные науки и дисциплины › Дебаты по Теории Относительности Эйнштейна › Неинвариантность Уравнений Максвелла
(Модераторы: peregoudovd, kkdil, E-Eater)
‹ Предыдущая тема | Следующая тема ›
Страниц: 1 2 3 4 ... 6Послать Тему Печать
Неинвариантность Уравнений Максвелла (Прочитано 14867 раз)
meandr
Ветеран форума
***
Вне Форума
Сообщений: 3827
КОСМОполит
Re: Неинвариантность Уравнений Максвелла
ответ #50 - 21.02.17 :: 12:42:22 pop писал(а) 21.02.17 :: 10:15:30:
ответьте ещё раз. Если на опыте измерены величины, которые при подстановке в уравнение дают истинность уравнения, то какие могут быть "трактовки"?
Если в это же уравнение ввести коэффициент в одно из ненулевых слагаемых, то уравнение не останется истинным. И никакими "трактовками" это не исправить.
Отвечу еще раз - первый на этой странице и последний, если не поймете (что скорее всего).
1. В уравнении напряженности (9) п.600 Трактата, составленном для ОБЩЕГО случая движущейся системы, предусмотрен "составной" скалярный потенциал
$\psi+\psi'$
где $\psi$ - обычный статический "кулоновский" потенциал - "собственный" потенциал поля заряда
$\psi'=\vec v \vec A$ - конвективный кинетический потенциал.
...
В современных обозначениях уравнение напряженности (9) в Трактате Максвелла
$\vec E=-\nabla\varphi-\nabla(\vec v \vec A)-\frac{\partial \vec A}{\partial t}$.
Это уравнение не во всех случаях адекватно опытам.
Поэтому
2. В современной ортодоксально-релятивистской теории используется раннее эфирное уравнение напряженности БЕЗ явного разбиения скалярного потенциала на "собственный" и конвективный потенциалы
$\vec E=-\nabla\varphi-\frac{\partial \vec A}{\partial t}$,
хотя наличие такого разделения с конвективным потенциалом неявно подразумевается преобразованиями Лоренца для потенциалов
В таком виде уравнения становятся адекватными опытам - но только в релятивистской трактовке понятий пространства и времени.
3. В классическом представлении пространства и времени уравнение Трактата с наличием конвективного потенциала становится адекватным только с коэффициентом 1/2 и определении вмп А как импульса движущегося поля "собственного" потенциала $\vec A=\varphi \vec v/c^2$
В решении.
Объяснение:
Найдите сумму и разность многочленов А и В. Запишите результат как многочлен стандартного вида.
1) Записать в одну строку, второй многочлен в скобках, между ними знак + или -.
2)Раскрыть скобки. Если между многочленами знак +, во втором многочлене знаки не меняются, если перед скобками знак -, меняются на противоположные.
3)Привести подобные члены.
4)Записать результат в стандартном виде, т.е., в порядке убывания степеней.
а) А = 5а + 3, В = - 3а - 4
5а + 3 + (- 3а - 4)=
=5а + 3 - 3а - 4=
=2а-1;
5а + 3 - (- 3а - 4)=
=5а + 3 + 3а + 4=
=8а + 7:
б) А = 7х² + 3х, В = - 2х - 1
7х² + 3х + (- 2х - 1 )=
=7х² + 3х - 2х - 1=
=7х² + х - 1;
7х² + 3х - (- 2х - 1 )=
=7х² + 3х + 2х + 1=
=7х² + 5х + 1;
в) А = 8b² + 2b - 4 В = 5 - 3b - 9b²
8b² + 2b - 4 + (5 - 3b - 9b² )=
=8b² + 2b - 4 + 5 - 3b - 9b² =
= -b² - b + 1;
8b² + 2b - 4 - (5 - 3b - 9b² )=
=8b² + 2b - 4 - 5 + 3b + 9b² =
=17b² + 5b - 9;
г) А = 11y - 12 - y³ В = 14 - 12y + y³
11y - 12 - y³ + (14 - 12y + y³ )=
= 11y - 12 - y³ + 14 - 12y + y³ =
= -у + 2;
11y - 12 - y³ - (14 - 12y + y³ )=
=11y - 12 - y³ - 14 + 12y - y³ =
= -2у³ + 23у - 26;
д) А = 6 + mn + 2 В = 4 - mn - m²
6 + mn + 2 + (4 - mn - m²)=
=6 + mn + 2 + 4 - mn - m²=
=m² + 12;
6 + mn + 2 - (4 - mn - m²)=
=6 + mn + 2 - 4 + mn + m²=
=m² + 2mn + 4.