1. Известно, что 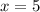 ,
, 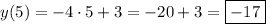
2. Известно, что 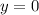 , тогда
, тогда 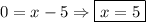
3. Обе точки имеют координаты 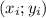 , причем при подставлении этих координат в уравнение функции, мы получаем верное равенство.
, причем при подставлении этих координат в уравнение функции, мы получаем верное равенство.
Смотрим на точку А: 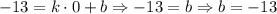
Отлично, уравнение известно теперь в таком виде: 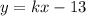 , в него подставим вторую точку и найдем
, в него подставим вторую точку и найдем 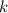 .
.
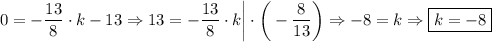
4. Решаем аналогично. Точка А: 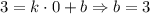
Уравнение уже в виде: 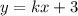
Точка B: 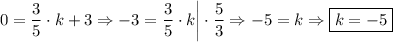
5. Условие симметрии относительно прямой 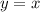 такое, что у функции
такое, что у функции 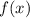 меняются местами область определения и область значений, то есть подставляя
меняются местами область определения и область значений, то есть подставляя 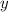 вместо
вместо  мы получаем по итогу
мы получаем по итогу  . При взаимно однозначном соответствии области определения и области значений (как в случае прямых) все вообще просто и работает везде.
. При взаимно однозначном соответствии области определения и области значений (как в случае прямых) все вообще просто и работает везде.
Что нужно сделать: есть 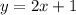 , делаем
, делаем
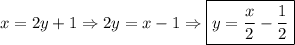
Заковыристая задача. Все очевидно, а доказать несколько сложновато.
Угол СС1В - прямой по построению как пересечение высоты СС1 со стороной АВ
Угол ВВ1С - прямой по построению как пересечение высоты ВВ1 со стороной АС. Отсюда угол СС1В и угол ВВ1С, равные 90⁰, совпадают по свойствам высот - все высоты треугольника пересекаются в одной точке. В данном случае для треугольника АВС - в точке А.
Отсюда треугольник АВС - прямоугольный.
Если угол В1=60 градусов, то
угол С1=90-60=30⁰,
а угол В=60⁰.
Для угла С осталось
С=90-60=30⁰