1)
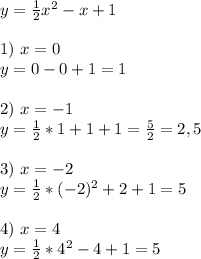
2)
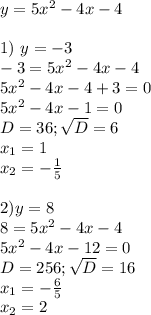
3)
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
5)
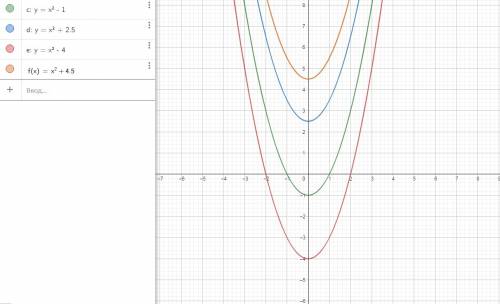
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)
x⁴ - 4x³ + 12x² - 24x + 24 = 0
(x⁴ - 4x³ + 4x²) + (8x² - 24x + 24) = 0
(x² - 2x)² + 8(x² - 3x + 3) = 0
(x² - 2x)² + 8(x² - 3x + 2,25) - 8 * 2,25 + 24 = 0
(x² - 2x)² +8(x - 1,5)² - 18 + 24 = 0
(x² - 2x)² + 8(x - 1,5)² + 6 = 0
(x² - 2x)² ≥ 0 при любых x
(x - 1,5)² ≥ 0 при любых x
Если обе скобки больше нуля, то после прибавления к ним числа 6 получим какое- то положительное число .
Если обе скобки равны нулю, то в ответе получим 6.
То есть, значение выражения в левой части всегда > 0 и не равно нулю ни при каких значениях x. Значит уравнение не имеет решений .
не знать
Объяснение:
чисиспиптпиарарарпрр