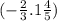
Большое количество задач такого типа решаются при формулы Ньютона-Лейбница:
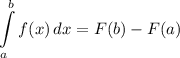
Поэтому, во-первых, нужно найти  и
и 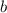 - абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
- абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
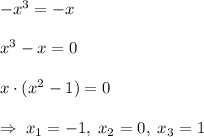
А так как есть целых три точки пересечения, то придется считать два интеграла: первый - от 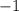 до
до 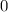 (как результат приравнивания функций:
(как результат приравнивания функций: 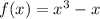 ), а второй - от
), а второй - от 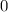 до
до  (здесь уже
(здесь уже 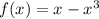 ):
):
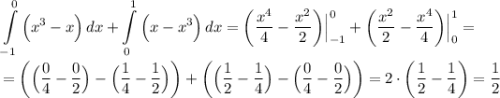
Значит, площадь искомой фигуры (состоящей из нескольких других фигур) равна 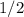 или
или 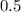 (каких-то квадратных единиц измерения), если перевести в десятичную дробь.
(каких-то квадратных единиц измерения), если перевести в десятичную дробь.
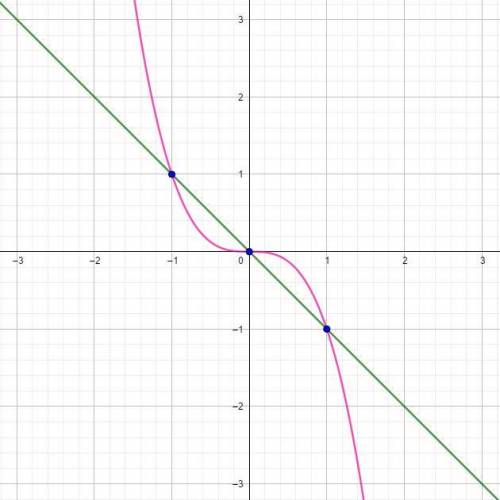
Большое количество задач такого типа решаются при формулы Ньютона-Лейбница:
Поэтому, во-первых, нужно найти и
и 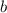 - абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
- абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
А так как есть целых три точки пересечения, то придется считать два интеграла: первый - от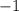 до
до 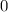 (как результат приравнивания функций:
(как результат приравнивания функций: 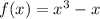 ), а второй - от
), а второй - от 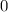 до
до  (здесь уже
(здесь уже 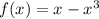 ):
):
Значит, площадь искомой фигуры (состоящей из нескольких других фигур) равна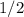 или
или 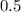 (каких-то квадратных единиц измерения), если перевести в десятичную дробь.
(каких-то квадратных единиц измерения), если перевести в десятичную дробь.
ответ: 0.5 .